Studoši

Zabe u onom zajednickom dokumentu imas taj zadatak rijesen

zaba Samo jedno pitanje za ovaj s L, S, N, T. Kad se racuna p(S=1|L=1, N=1), u nazivniku N predstavlja ukupan broj primjera za koje je L=1 i N=1? Da je npr bio jos jedan primjer recimo L=1, N=1, S=0, T=0, onda bi taj N u nazivniku bio jednak 2?

bearyn da, tocno to

Kako se ovo rješava, odnosno što se uvrštava za mi kod izračuna p(x|y=1)?

zaba Čemu služiju izračuni P(T=0 | N=1) i P(T=1 | N=1)?

ygerg11 da izracunas zajednicku vjerojatnost (koja u sebi ima P(T|N)), ali u ovom slucaju je njihov zbroj jednak 1 pa nisu ni bitni

zaba aha to sam i mislio, hvala 😊

Zna netko riješiti? Svi su mi OK, ali s ovim se mucim već par sati.

Hvala!

pushPop
Zna netko ovaj? U zajedničkom dokumentu ga je riješila kolegica, ali nije sigurno da je dobar postupak.

Ima li netko rijesen zadatak sa cloudy/rainy/sprinkler/wet?

Murin Pitaj u dokumentu, bit će preglednije a i prof će komentirati

Murin


Na drugoj slici je donji dio razlomka

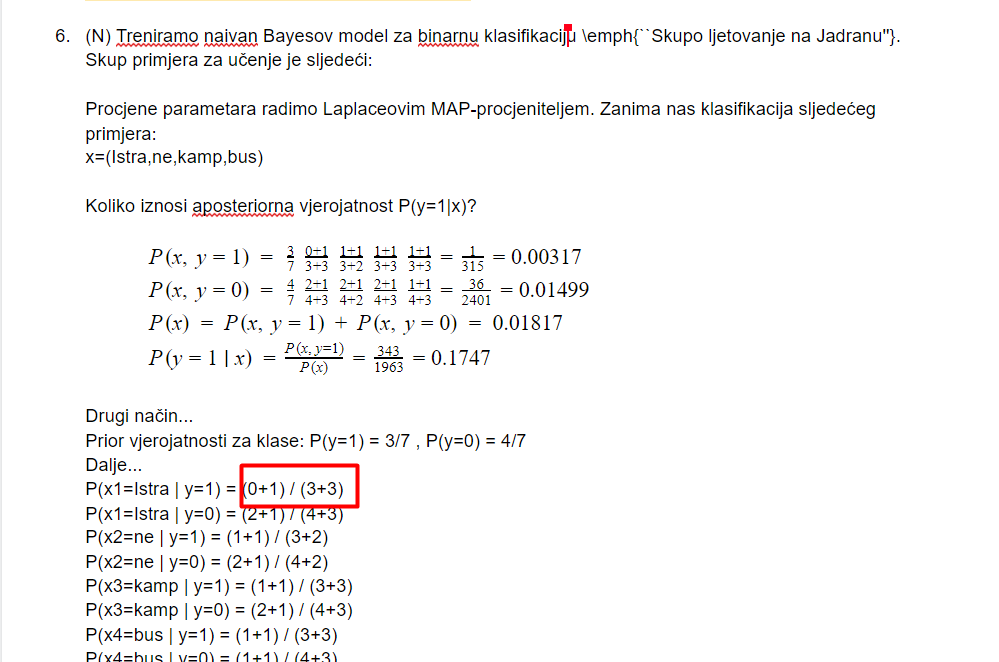
kako se dobiju ove vrijednosti? moze netko objansiti?

enaiks Nazivnik… gledaš u tablici sve retke di je y=1, a x1=Istra. Takvih redaka je 0. Dodaš 1 zbog Laplaceovog zaglađivanja. Brojnik… ukupno imaš 3 retka s y=1. Još dodaš 3 jer imamo 3 vrijednosti za x1, ovo isto radiš zbog Laplaceovog zaglađivanja.

ima netko formule za ove zadatake?

enaiks broj parametara kod logisticke regresije se ne mijenja kada broj klasa raste? recimo da imamo 5 klasa umjesto 2, opet bi br parametara ostao n+1?

enaiks za ovaj drugi zadatak, broj parametara LR je n+1, a broj parametara Gauss Bayesa je n*(n+1)/2 + 2n + 1. Kad ubacis i oduzmes (jer te trazi koliko ovaj drugi ima vise param od prvog) dobijes 5150

enaiks Ne, bio bi 5*(n+1)

Zna netko postupak za ovaj?

edit: naso u dokumentu

zaba mozes objasniti u ovom xyz yadatku, kako si dosao do te formule?

enaiks koje formule? zajednicku distribuciju dobjes u zadatku. ides po njoj i u svakom cvoru fiksiras varijablu na neku vrijednost ovisno o distribuciji tog cvora (npr za x ces s vjerojatnosti 0.2 uzeti da je x=1, a s 0.8 da je x=0, itd..) to napravis 1000 puta i dobit ces neke ntorke npr (x=1, y=1, z=0), (x=0, y=0, z=0), … na kraju odbacis sve osim onih kojima su x=1 i z=1. ocekivano je da ce ti takvih parova ostati: br primjera puta vjerojatnost da je x=1 puta (vjerojatnost da je z = 1 i y = 0 ili vjerojatnost da je z = 1 i y = 1)

znaci samo sam iskoristila zajednicku distribuciju

postoji li skripta Vrednovanje modela?

enaiks https://arxiv.org/abs/1811.12808 Nije službena skripta, ali će poslužit. Pročitaš ono što ti treba.