Studoši

Ovaj zadatak je iz https://www.fer.unizg.hr/_download/repository/RR_-_07.09.2018._-_HR.pdf ovog ispita…

Moje pitanje glasi… šta se točno mijenja kada mi imamo neku drugu aktivacijsku funckiju kod onih formula koje imamo u podsjetniku. Moja teorija da se mijenjaju “EI” dijelovi jer oni u sebi imaju “y - ( 1 - y )” što je zapravo derivacija sigmusoida. Stoga sada bi umjesto “y - ( 1 - y )” trebalo staviti valjda derivaciju te neke druge funkcije (npr kod ovog zadatka tanh)…

Takoder… primjetite da je on u “Napomeni” na ispitu stavio kako mozemo taj tanh izrazit preko sigmoida stoga to me navodi na zakljucak da se nekako iz derivacije sigmoida moze zakljucit derivacija tanh. Daj ako skuzite, riješite cijeli zadatak i slikajte postupak

Imamo jedan rješen zadatak (OVO NIJE RJEŠENJE ZADATKA IZNAD, NEGO DRUGI ZADATAK iz ovog ispita …https://www.fer.unizg.hr/_download/repository/RR_-_6.9.2013._-_HR.pdf )di je aktivacijska funckija “Adaline” tj. linearna funckija čija je derivacija očito “1” jer je Adaline samo pravac, stoga “EI” formula postaje EI = EA. Evo slika koja to pokazuje … (zaokruzeno vam je na slici)

teslaFan Moja teorija da se mijenjaju “EI” dijelovi jer oni u sebi imaju “y - ( 1 - y )” što je zapravo derivacija sigmusoida. Stoga sada bi umjesto “y - ( 1 - y )” trebalo staviti valjda derivaciju te neke druge funkcije (npr kod ovog zadatka tanh)…

I da i ne. Ne mijenja se samo y (1 - y) jer bi to trebalo biti \sigma(x) (1 - \sigma(x)). Mijenja se i ono prije, aktivacijska funkcija ne mora u derivaciji imati samu sebe pa biti izražena tako.

A tanh je samo sigmoid s kodomenom \langle -1, 1 \rangle centriran u 0. Tj., tanh(x) \equiv 2(\sigma(2x) - 0.5)

Jedno pitanje za brisanje čvora u B-stablu. Primjetio sam da u prezentaciji piše da kada brišemo element koji nije “leaf” onda nađemo njegovog prethodnika te ga stavimo na njegovo mjesto… sljedeća slika sa preze to prikazuje

Ono što mene mući je da sam na internetu našao algoritam gdje se gleda i prethodnik i sljedbenik… otprilike ovako

1. Pogledaj prethodnika i upiši njega samo ako nakon brisanja tog pretodnika će i dalje biti više od minBrojKljuceva u cvoru
2. Pogledaj sljedbenika i upiši njega samo ako nakon brisanja tog sljedbenika će i dalje biti više od minBrojKljuceva u cvoru
3. Ako 1. i 2. uvjet padnu (nakon brisanja će biti manje od minBrojKljuceva) onda je svejedno hoćeš li odabrat prethodnika ili sljedbenika

Zašto je ovo uopće bitno?
Zato što se može dogoditi situacija slična sljedećoj (isto iz prezentacije slika). Pogledajte (f) korak tj. korak di je “Delete 16”.

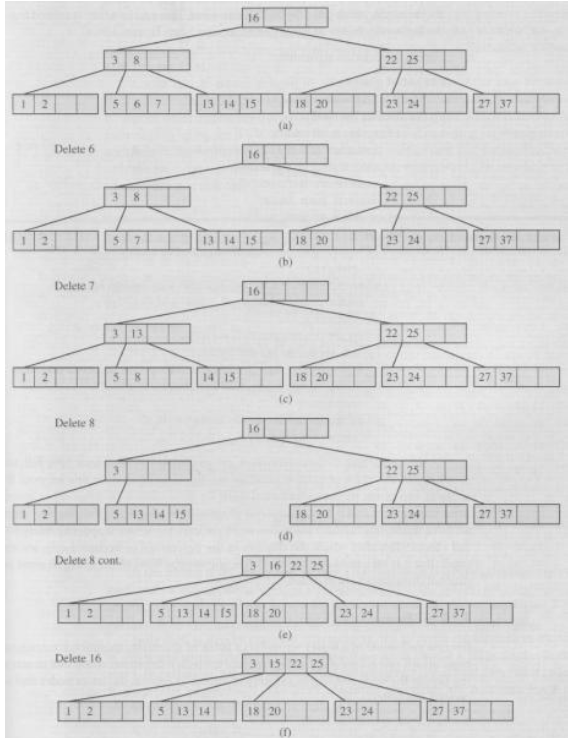
Ovdje se algoritam iz prezenacije ne bi mučio, jer iz čvora (5,13,14,15) možemo nešto obrisati, ali kada bi situacija bila obrnuta npr. da imamo čvor (5,13), a desno od njega (18,20,21) onda bi iz ovog desnog čvor mogli obrisati neki element, ali algoritam iz prezentacije to ne bi napravio

Hoćete li vi rješavat uvijek gledati prethodnika (prezentacija algoritam) ili ćete prethodnika pa sljedbenika (internet algoritam) ?

Nakon još malo proučavanja mislim da je najbolje koristiti algoritam iz prezentacije (znači uvijek uzimati prethodnika). Čisto zato što se onda možete pozvati na prezentaciju ako će biti kakvih problema. Takoder, vizualizator koji je profesor preporučio tj. https://www.cs.usfca.edu/~galles/visualization/BTree.html isto uvijek uzima prethodnika.

Koje prezentacije s ferweba su bolje? One kojih ima 9 ili one kojih ima 13 (P01-predavanja)?

Bobicki Prilično sam siguran ove s 13. Po tima ću bar ja učiti, možda je do ukusa.

Ovo je postman zadatak (znaci najkrači eulerov ciklus) … jel mi moze netko objasnit šta će nama ovaj graf desno (bipartit graf). U prezentaciji kao piše da njega nacrtamo i riješimo “optimal assignment” tj. pronađemo optimalne parove, ali ja stvarno ne vidim kako mi to možemo vidjeti iz tog grafa. Može neko objasnit? Ili ima li neki bolji način od toga?

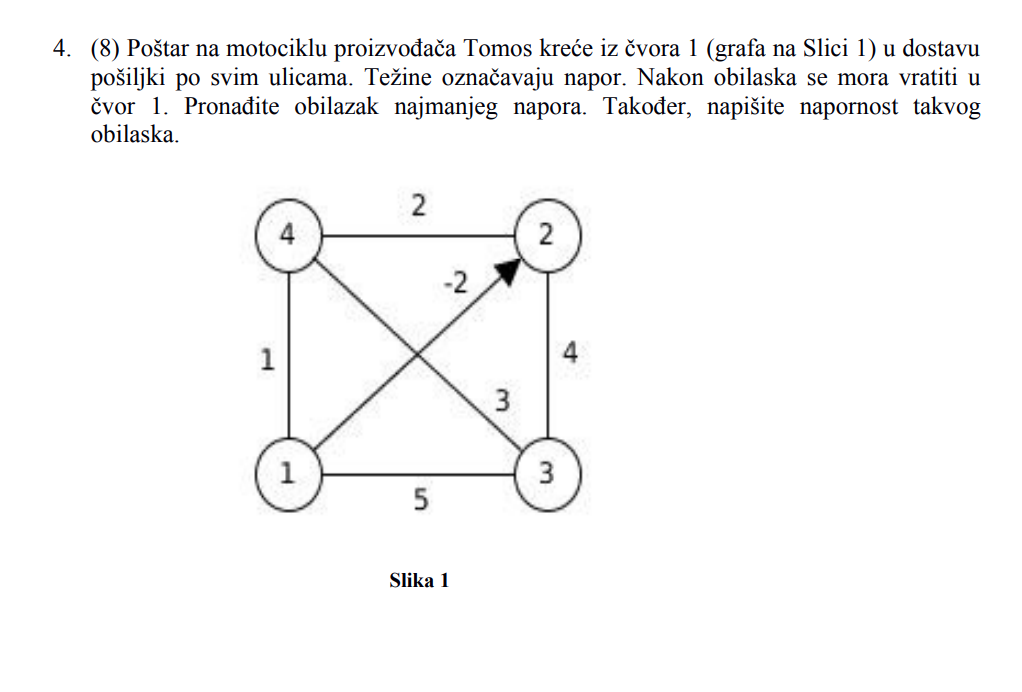
Jel zna netko ovaj rješiti iz https://www.fer.unizg.hr/_download/repository/ZR_-_10.2.2020_-_HR.pdf
Jer očito ima jedan directed graf pa ne znam jel možemo to duplicirat?
Čak i da možemo duplicirat jel duplicirat u suprutnom smjeru ili? I ako dupliciram u suprutnom smjeru jel onda stavim “2” i li “-2” … daj molim netko riješi pa nek slika

teslaFan Zaboravio sam sliku uploadat…

teslaFan Što se tiče ovog tvog primjera mislim da rješavaš identično kao i kad je graf neusmjeren, osim što kod traženja parova vrhova koji su najbliži (recimo pomoću WFI) u obzir uzimaš usmjerenost ovog jednog brida. I ako on sudjeluje u najkraćem putu između dva vrha koja povezuješ, obavezno ga uduplaš u istom smjeru u kojem je u početnom grafu (što po meni jedino logično ima smisla, ako se tim bridom može ići u samo tom smjeru).

Početno uduplavanje svih neusmjerenih bridova mi nema smisla, jer se tada svi neusmjereni obavezno moraju proći dvaput, što mi se ne čini najkraćim putem.

Kolko sam skuzio kad daju usmjereni graf svi bridovi “bez strelica” su dvosmjerni, znaci u ovom slucaju dupliciras sve ostale osim ovog usmjerenog pa imas npr. brid (1, 3) i (3,1) oba s weightom 5.
Tako dobijes da su vrhovi 1,3 i 4 parnog stupnja pa je lagano dalje prosetat postara…

@teslaFan fPolic Zna li netko rješiti sedmi sa ovogodišnjeg LR?

https://www.fer.unizg.hr/_download/repository/LR_-_10.7.2020.pdf

Traži se najkraći put od A do D, s time da je graf usmjeren i ima negativne težine. Dakle to bi trebalo Bellman Fordom rješavat ako se ne varam. Ali koliko vidim, u grafu postoji negativan ciklus C->G->C pa Bellman Ford ne može pronaći rješenje.

Imate li ili netko drugi ideju kako s ovim?

TentationeM Ja sam na ispitu isto dobio negativni ciklus CGC s Bellman Fordom i prema bodovima mi se cini da je priznao to.

fPolic A što si napravio, našao put izbjegavajući taj ciklus, nisi ulazio u ciklus, ili si napisao da nema rješenja? Koliko znam u praksi je obično odgovor ovo zadnje, ali to se lako može izbjeći pa ne kužim zašto nisu napisali npr. da se svaki čvor smije posjetiti najviše jedamput.

Meni je ovak ispalo Bellman Fordom, valjda je okej (vidim da fale C = 6 samo)

M̵̧̩͑̀͝î̶͍̉ć̴̝̾́̀o̶̺̟̣͂̽ Znaš možda MI 2014 5. pod c). To je tvoja struka pa ne bi problema trebalo biti 😅 Ovako na prvu ne pronalazim postupak u materijalima.

https://www.fer.unizg.hr/_download/repository/M_-_20.11.2014._-_HR.pdf

TentationeM Riješit ću to danas, al ovdje imamo problem što nije definirano početno stanje.

Sve što se događa je da akumuliraš gradijent oba ulaza i onda to primijeniš na težine. Odabir težina za 1. i 4. značajku je nebitan (vidljivo je iz ulaza da su redundantne), a težine za 2. i 3. značajku bi inicijalizirao na 1 (radi jednostavnosti), a pomake na 0.

Dakle,

w = \begin{bmatrix} 0 \\ 1 \\ 1 \\ 0 \\ \end{bmatrix}, b = \begin{bmatrix} 1 \end{bmatrix}

Uzmite u obzir da su meni ulazi retčani, a ne stupčasti vektor, pa su ove veličine potencijalno transponirane. Gradijent je također elementaran - ako pretpostavimo da koristimo MSE, onda je gradijent izlaza \vec{o} - \vec{y}, gdje o pretpostavlja izlaz mreže a y labelu, nazovimo taj vektor \vec{d}, pa su gradijenti po parametrima

\frac{\partial{L}}{\partial{w}} = \begin{bmatrix} i_0 \cdot \vec{d} \\ i_1 \cdot \vec{d} \\ i_2 \cdot \vec{d} \\ i_3 \cdot \vec{d} \\ \end{bmatrix}, \frac{\partial{L}}{\partial{b}} = \begin{bmatrix} \vec{d} \end{bmatrix}

Mislim da uz stopu učenja 0.1 ovo sigurno konvergira, pa se može uzeti ili ta stopa učenja, ili 0.5 koji linearno decaya za 0.1 po epohi. Dodatno: U slučaju batch learninga na malom datasetu može i veći learning rate, npr. 1.

Konkretan postupak, kao i ispravke ću kasnije priložiti, jer trebam još jednom proći to gradivo pa idem na rješavanje zadataka, a na poslu sam trenutno. Ali sve što treba ovdje je računati isto kao on-line learning, akumulirati gradijente, i tek nakon što se prođe kroz cijeli dataset njihov prosjek oduzeti težinama.

@TentationeM

Evo, izvrtio sam 2 epohe, može se i 3. (treba uputa koji je prag za kraj treninga). Stopa učenja je 1. Gradijenti se akumuliraju kao aritmetička suma.

EDIT: Isto tako, bez akumulacije gradijenata se može koristiti onaj loss koji minimizira L2 normu vektora pogreške. Međutim gradijent toga ima sjebaniju formulaciju, takav tip lossa je striktno regresijski i u praksi se to ne radi (već se radi akumulacija gradijenta, kao što sam ja napravio). Oni također spominju minimiziranje zbroja kvadrata, ovo se u praksi ne radi jer gradijenti eksplodiraju za veće datasetove, već se koristi uprosječivanje da su gradijenti neovisni o broju primjeraka u grupi.