Studoši

Cvija Pošto ne mogu urediti, mislim da je ovdje došlo do zabune. Algoritam koji se koristi u zadacima je na 31 slajdu, to je onaj sa poljima, na 37 slajdu je sa stablima, možda sam tu pogriješio, ispričavam se na pogrešci.

saitama

Bobicki

member
Evo sad ću proći po algoritmu pa možda bude jasnije

Zadatak od kolege
member
Znači, na početku imamo ovakvo stanje
\begin{bmatrix}root && 1 && 2 && 3 && 4 && 5 && 6 \\ next && 1 && 2 && 3 && 4 && 5 && 6\\ length && 1 && 1 && 1 && 1 && 1 && 1\\ vertices && 1 && 2 && 3 && 4 && 5 && 6 \end{bmatrix}
Sad radimo Union(1, 2)
Po algoritmu, xs = root(x) = root(1) = 1
ys = root(y) = root(2) = 2

xs i ys nisu jednaki pa provjeravamo njihove duljine (lenght)
ys nema veću duljinu od xs (obje su 1) pa znači da radimo sljedeći set komandi
length[xs] += length[ys]
root[ys] = xs
svi u polju u kojem je korijen bio ys, za korijen im postavi xs
na kraju zamijeni sljedećeg od xs i sljedećeg od ys
Nakon tog seta operacija se dobije
\begin{bmatrix}root && 1 && 1 && 3 && 4 && 5 && 6 \\ next && 2 && 1 && 3 && 4 && 5 && 6\\ length && 2 && 1 && 1 && 1 && 1 && 1\\ vertices && 1 && 2 && 3 && 4 && 5 && 6 \end{bmatrix}
Onda ide Union(4, 3), isto sve
\begin{bmatrix}root && 1 && 1 && 4 && 4 && 5 && 6 \\ next && 2 && 1 && 4 && 3 && 5 && 6\\ length && 2 && 1 && 1 && 2 && 1 && 1\\ vertices && 1 && 2 && 3 && 4 && 5 && 6 \end{bmatrix}
Nakon Union(2, 3) [xs = 1, ys = 4]:
\begin{bmatrix}root && 1 && 1 && 1 && 1 && 5 && 6 \\ next && 3 && 1 && 4 && 2 && 5 && 6\\ length && 4 && 1 && 1 && 2 && 1 && 1\\ vertices && 1 && 2 && 3 && 4 && 5 && 6 \end{bmatrix}
Te na kraju nakon Union(1, 6)
\begin{bmatrix}root && 1 && 1 && 1 && 1 && 5 && 1 \\ next && 6 && 1 && 4 && 2 && 5 && 3\\ length && 5 && 1 && 1 && 2 && 1 && 1\\ vertices && 1 && 2 && 3 && 4 && 5 && 6 \end{bmatrix}
Nacrtat se može pomoću ove tablice

Jel smijemo kao što je objašnjeno u word tutorialu na materijalima svaki put prebacit u oblik standardne maksimizacije tako da nikad ne trebamo rješavat dvofaznom metodom?

Ducius Ovo me toliko zbunjuje. U prezi piše da ako imamo negativne koeficijente s desne strane, oni se moraju pomnožit s -1 i postat pozitivni i onda valjda po tome moramo radit dvofazni jer ne smijemo imati -7 na desnoj strani. Ali u tutorialu je normalno riješeno s negativnim koeficijentima i to se rješenje lijepo poklapa sa uvjetima. Wtf.
Da usporedim, probala sam riješiti taj zadatak iz tutoriala sa jednofaznim i dvofaznim simpleksom.
S tim da sam dvofazni pratila kak je prof rješavao na auditornima i moguće je da sam negdje pogriješila. Uglavnom, sa dvofaznim dobijem manju vrijednost, a sa jednofaznim veću. Wtf again.

Je li potrebno raditi onu PI tablicu za algoritam WFI ili se moze i bez?

Murin Možeš i bez al će ti biti skoro nemoguće pratiti napamet

Murin U ZI 13/14 (5. zadatak) tražili su ispis D i PI tablice, a u ostalim WFI zadacima narednih godina nije ništa pisalo osim da se provede WFI, tako da ne znam da li će tražiti obje tablice za sve bodove.

M̵̧̩͑̀͝î̶͍̉ć̴̝̾́̀o̶̺̟̣͂̽

ili ja imam big brain za tu konkretnu vrstu zadatka ili ima neki detalj kojeg nisam svjestan

do sad sam dobivao sve tocne rezultate tak da idk

Murin Pi tablica ti služi da pratiš prethodne čvorove, bez nje kod svakog updatea moraš pratiti prethodni čvor napamet ako se promijeni. Ako ti možeš pratiti samo tako n² stanja svaka čast, ali generalno nemaju tako svi memoriju, a i ispravljači bi mogli obratiti manje pažnje na rješenje u slučaju da oni pogriješe u projeni kad ne mogu pratiti ispravnost rješenja ako je drukčije od njihovog, i onda ti skinu bodove bzvz.

Murin Dobiju se dobri rezultati i bez Pi tablice ako su mali grafovi. Pi tablica bilježi najkraći put između dva vrha. Za imalo veći graf nemoguće je zapamtiti koji je najkraći put između dva vrha u nekoj iteraciji.

little reminder na ovo https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
ima i disjoint sets skroz dole

Kolko vam ispadne duljina puta u ZI od prosle godine u zadnjem zadatku?

saitama 77?

M̵̧̩͑̀͝î̶͍̉ć̴̝̾́̀o̶̺̟̣͂̽

Ovo kaj si opiso mi zvuci dost komplicirano naspram onog kaj ja radim

Ja idem ovak-ako imam cvorove a….z, imat cu po jednu matricu za svaki cvori pocetnu D0, za prvu matricu kazem neka mi je K=A i onda gledam za i,j element nove matrice je li stara[i,j]>stara[i,K]+stara[K,j], uzimam ono sto je bolje i tjt. element po element i gotovo rjesenje, s tim da neke stvari odmah mozes upisat bez racuna..-

adidas
najveca kaj sam rjesavao je bila 5×5, nezz dal ce stavit nes vece od toga a da ne bude neusmjereno

Murin To i možeš, jer algoritam provjerava samo matricu D, međutim nećeš moći tako lagano nacrtati graf.

EDIT: + ono što mi je flashbackalo, neki ljudi (i.e. npr. ja) brže vrte algoritam gledajući graf nego tablicu.

Murin Zapravo možeš napraviti D tablicu bez Pi kako si opisao. Jedino što onda znaš samo min udaljenost između vrhova X i Y. Ne znaš odmah koji je to put ( kojim vrhovima prolazi najkraći put ) nego moraš gledati u graf i napikavati koji vrhovi bi dali takvu udaljenost. Iz Pi tablice možeš odmah iščitati i puteve.

Zna li netko ovo?
I bi li se odgovor promijenio da graf na slici ima negativne težine na nekim bridovima?

DaL

da ne

DaL I bi li se odgovor promijenio da graf na slici ima negativne težine na nekim bridovima?

da ne

M̵̧̩͑̀͝î̶͍̉ć̴̝̾́̀o̶̺̟̣͂̽ sto nije odgovor ne i ne?

Npr dodamo svima 7. Gledamo put izmedu F i C, prije je bio 3+2, no sada imamo 8+7<3+7+2+7

Ako se ne varam, ovo nije dobro riješeno:

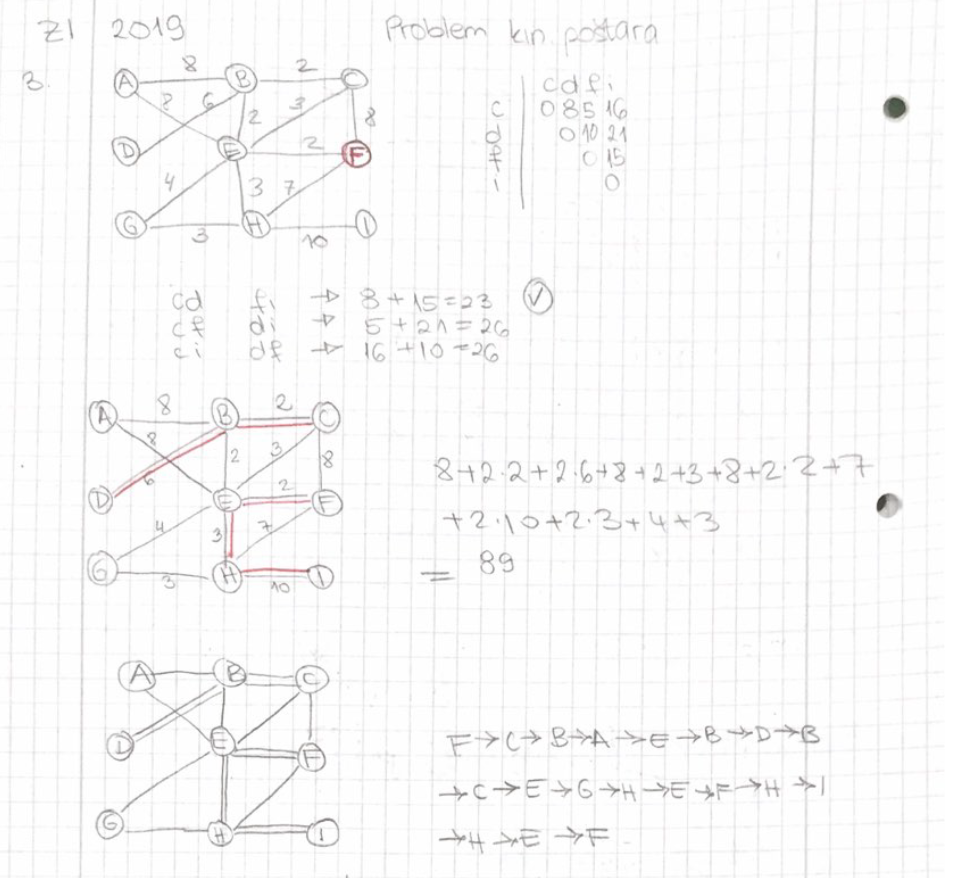
Trebalo bi dodati direktne bridove između C i D te F i I, a ne povezati sve vrhove na najkraćem putu između njih.

in1 Uh ne? Legit je u prezentacijama riješeno tak i nema smisla izmišljati nove bridove

M̵̧̩͑̀͝î̶͍̉ć̴̝̾́̀o̶̺̟̣͂̽ Hmmm, siguran?
Meni ovdje izgleda kao da je direktno spojeno

in1 Ajde malo bolje pogledaj, linija je zaustavljena u točki i nastavlja iz točke

M̵̧̩͑̀͝î̶͍̉ć̴̝̾́̀o̶̺̟̣͂̽ Oke, nvm, naletio sam na drugi primjer iz prezentacije gdje se vidi:

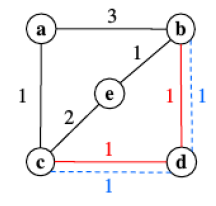
Dakle, dobro je rješenje iz pdfa