Studoši

ink Nisam slikao, niti sam siguran da mi je točno, ali ja sam to ovako:
Okviri su dio fizičkog spremnika, a stranice su dio logičkog adr. prostora. Adrese su 16-bitne,a veličina stranice (jednaka veličini okvira) je 16 [imath]\Rightarrow r=12, p=4[/imath] .
Broj okvira je onda veličina spremnika podijeljena s veličinom okvira: 16KB/16B = 1024
Maksimalno stranica je onda 2^r = 2¹² = 4096 .
Najviše zapisa u tablici prevođenja je ako su svi okviri zauzeti, a njih je 1024.
Minimalno bitova potrebno za adresiranje 1024 ( 2¹⁰ ) okvira je 10.
Najveća veličina spremnika koju sustav može adresirati je ako je broj okvira jednak broju stranica: 4096 * 16B = 65536 B = 64 KB .
U takvom, najvećem sustavu je onda 64KB / 16B = 4096 okvira

Rene

kako su se ova 2 trebala rj?

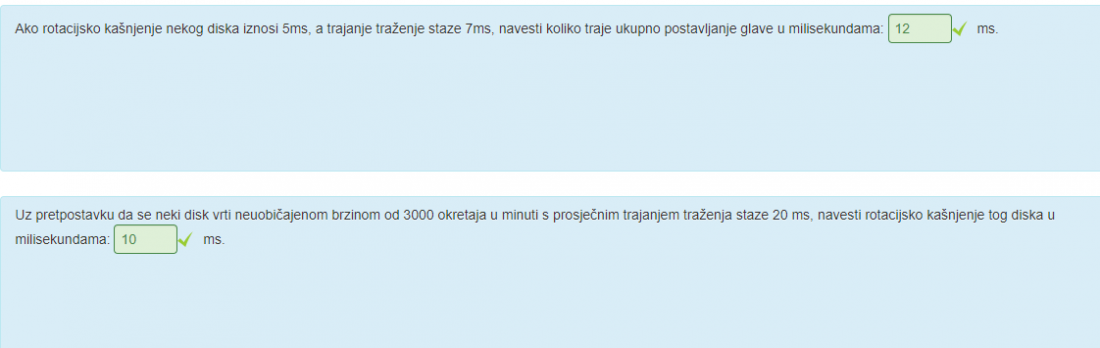
Sicsile U petom se samo zbroje vrijednosti. U sestom se 3000 okretaja/minuti pretvori u 50 okretaja/sekundi, onda Tr iznosi 1/50s odnosno 20ms. Rotacijsko kasnjenje je Tr/2, pa se dobije 10ms. Ova informacija o prosjecnom trajanju trazenja staze je nepotrebna.

Sicsile
Rotacijsko kašnjenje je definirano kao [imath]\frac{T_R}{2}[/imath], odnosno pola vremena okretaja.
Dakle u 5. je odgovor 12 ms jer ne treba još jednom dijeliti s 2, a u 6. je 10 ms jer se traži vrijednost podijeljena s 2.

Edit: Takve su oznake i nazivi na prezentacijama.
U videu Jelenković [imath]\frac{T_R}{2}[/imath] zove prosječno rotacijsko kašnjenje i označava s [imath]\overline{T}_R[/imath].

6. isto tako…3000/60 je 50 i 1/50 je 0.02 što je 20 ms i takav postupak je i slajdovima predavanja..da…pa jos kroz 2

niknik ali ako trazis prosjecnu vrijednost moras jos tih 20 podijeliti s 2 i dobijes 10 sto je tocan odgovor

King Geedorah zar nije da se u petom uzima Tseek tj 7ms + Tr/2, a u 6. Sam mislio da da treba uzet rotacijsko kasnjenje a ne srednje rotacijsko kasnjenje

std::popcount
u 6. Pise navesti rotacijsko kasnjenje, a ne prosjecno rotacijsko kasnjenje i koliko vidim u skripte ima razlike izmedu tog dvoje pa sad ne znam.

Sicsile Moj ti je savjet poslati mail, do sada su uvijek izlazili u susret ako je bilo nekih problema i nedoumica tako da nemas sto izgubit.

Sicsile u 6. Pise navesti rotacijsko kasnjenje, a ne prosjecno rotacijsko kasnjenje i koliko vidim u skripte ima razlike izmedu tog dvoje pa sad ne znam.

Jel slao netko mail za ovo posto prof. ne odgovara na upit na teamsu?

Kako ide postupak za ovaj? Točno rješenje je 30 ms.

koode7 pola boda fali za prolaz bez završnog 😩

Ako je netko radio po Jelenkovićevoj skripti - ima li negdje rjesenja zadataka?

Ruasonid On obicno u videima na svom yt kanalu rjesi zadatke iz skripte

viliml Što se tiče ovog pod c), tu je odgovor valjda isti kao pod b). Tablica prevođenja ima redaka koliko i logički adresni prostor stranica.
d) sam slao mail, odgovorio mi je kako bi 10 bitova značilo da imamo fiksan RAM i da ne možemo dodati još RAMa.. Pa je tu odgovor onaj r, 16 - p, ovdje 12 čini mi se

viliml Jel bi mogao netko objasniti taj zadatak ukratko?

Peter Jordanson

Okviri se odnose na memoriju koja je fizički prisutna. Okvira ima 16 KB / 16 B = 1024

Adresa je 16-bitna, što znači da je logički adresni prostor 2¹⁶ B = 65536 B = 64 KB.
Svaki proces može koristiti cijeli logički adresni prostor. Stranica ima 64 KB / 16 B = 4096

Tablica prevođenja može imati zapis za svaku stranicu. Dakle zapisa je 4096.

Neovisno o količini memorije koja je prisutna, format zapisa u tablici prevođenja je uvijek isti. Kako ona mora podržavati slučaj kada maksimalno memorije (broj okvira = broj stranica), ona mora moći adresirati svih potencijalnih 4096 okvira. Za adresirati 4096 okvira treba log₂(4096) bit = 12 bit.
Drugi način računanja: Adrese su 16-bitne, ali kako su stranice velike 16 B, najnižih log₂(16) = 4 bitova adrese ne mijenja kojoj stranici adresa pripada, pa za adresiranje okvira treba 16 - 4= 12 bita.

Maksimalna veličina spremnika je jednaka veličini logičkog adresnog prostora, 64 KB.

U tom slučaju je broj okvira jednak broju stranica, jer su logički i fizički adresni prostori jednake veličine: 4096.

Sjecam se da je Golub na predavanju govorio da bacimo pogled na stare ispite da dobijemo dojam sto se trazi na predmetu (i da ce i on to radit s nama na predavanju). Gdje se mogu nac stari ispiti jer na ferwebu ne vidim nista?

AcoSofronijevic https://github.com/studosi-fer/OS/tree/master/ispiti/zi