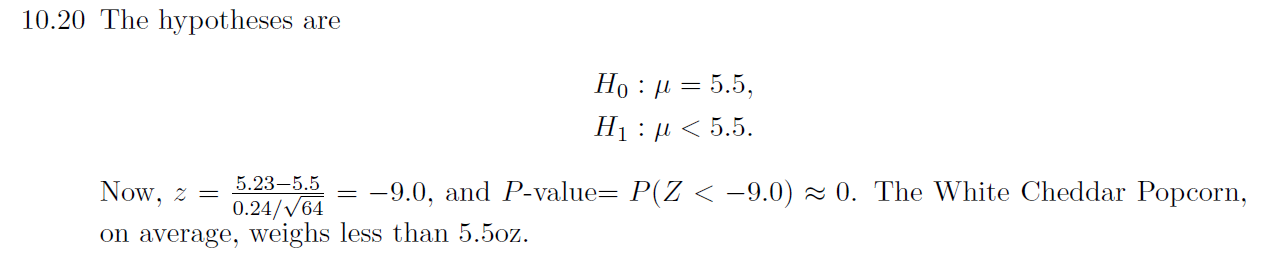[SAP] O predmetu
JBear
latica Bit će, ali nama na 3. godini iz nekog razloga skoro ni jedan predmet nije upisan, vjerojatno će sutra biti upisani
boogie_woogie
Hoćemo li imati neki podsjetnik na ispitima iz ovoga?
InCogNiTo124
PeroPerica
feudalac Rok je tezi od ispita, ali ne znacajno, vjerojatno zato sto je sve gradivo unutra. Ugl, bude zadataka u kojima stvarno moras dobro razmislit, al nista van okvira toga sto se uci.
Joskica
jel ima netko jos starih ispita osim onog iz 2017.?
WP_Deva
Predavanje 20.10. je isteklo na Teamsu za skinut, je li netko možda skinuo to predavanje, i je li netko slučajno snimio ono predavanje 6.10. koje nije bilo uopće snimano?
gladiator
Je li netko riješio MI/ZI sa stranice predmeta da podijeli rezultate?
latica
gladiator bump
sheriffHorsey
U popisu literature su kao 7. predavanje navedeni postupci ponovnog uzorkovanja, a zadnja prezentacija je linearna regresija. Koje od tog dvojeg onda ulazi u međuispit?
swish41
sheriffHorsey linearna regresija, al ne cijela ppt, zadnje što ulazi je Test o linerarnosti
error
Možemo li koristiti kalkulator na MI?
kix7
error da
gladiator
ne frajeru, donesi abakus i logaritamske tablice
error
gladiator hvala<3
a moze sad neki odgovor koji nije ovako braindead?
InCogNiTo124
error a moze sad neki odgovor koji nije ovako braindead?
Ne moze, pa na statistickoj analizi si, zakljuci iz odgovora kolege xD
error
Fish99 hvalaa
ppooww
Koja poglavlja za linearnu regresiju iz Walpolea treba znat? 11.1-11.9 ?
Lyras

Je li rješio možda ovaj netko? Nije mi baš razumljiv zadatak
spenadla
Rene
spenadla Da nadopunim i b) dio zadatka:
Snaga testa je 1-\beta , \beta je vjerojatnost da ne odbacimo H0 iako je H1 ispravna.
Iz tablice pročitaš -z_{0.05} = -1.645 , pa to preračunaš u kritičnu vrijednost \bar{x} = 5.375 . Dakle, nultu hipotezu odbacuješ kad je vrijednost z-statistike manja od -1.645 odnosno kad je srednja vrijednost uzorka manja od 5.375.
\beta je sada vjerojatnost da srednja vrijednost uzorka bude VEĆA od 5.375 (jer tada nećeš odbaciti H0), ako je ispravna hipoteza H1 pa računaš:
\beta = P( \bar{X} > 5.375 | H_1 istinita) = P(\frac{\bar{X}-5.3}{\sigma / \sqrt{n}} > \frac{5.375-5.3}{\sigma / \sqrt{n}}) =P(Z > 0.98) = 0.1635
Snaga testa je onda 0.8365. (nek neko ispravi ako griješim)
Tompa007
spenadla disi naso ta rjesenja ?