[IRG] Gradivo
Sicsile
VolimStopala🇻🇦🇭🇷 ja sam to ovako. Zar ima neki brzi nacin?
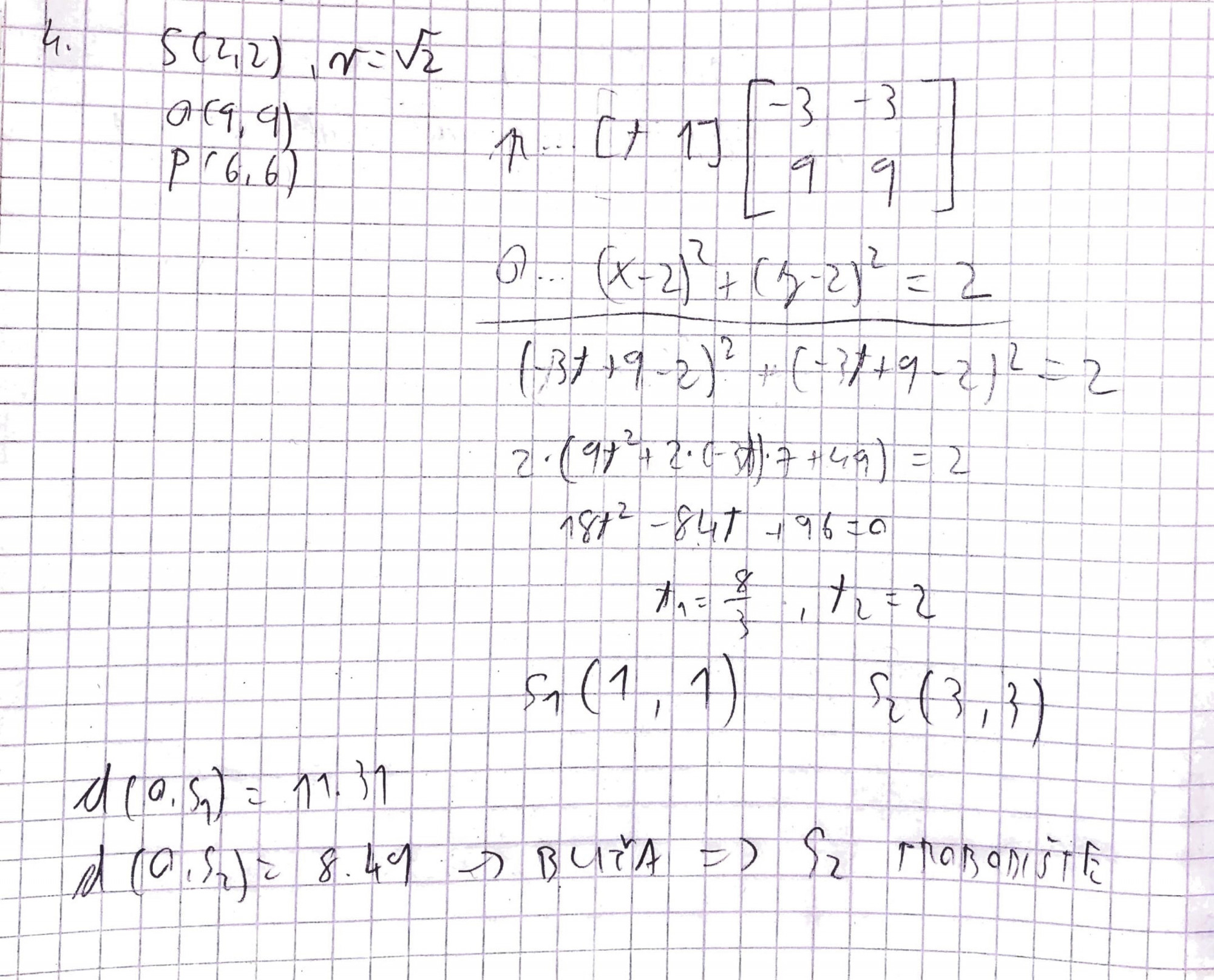
domagojj
Sicsile ne, to je to
[obrisani korisnik]

zašto nam ovdje nije bitan redoslijed vrhova?
domagojj
[obrisani korisnik] mislim da je to samo naputak da ne gubimo vrijeme na provjeru jel dobro zadan zadatak.
Mihael
jel netko rijesavao wiki zadatke na linuxu
Emma63194
Prošlogodišnji ZI (doduše, mi nismo imali MI pa je u ispit ulazilo cijelo gradivo, ne znam kako je ove godine):




Prošlogodišnji JIR:




Djelomično s koronskog roka:

Poslao mi je jedan kolega ovo pa evo, nadam se da će nekome pomoći kod pripreme za ispit!
angello2
Emma63194 neka dobra dusa da slika postupke za ovaj zavrsni?
batman3000

Zna li netko ovaj?
domagojj
batman3000 znaci kut između promatraca i odbijene zrake je 10 stupnjeva, a intenzitete izracunas odvojeno.
Prvi slucaj kd=1 a I=1, drugi slucaj kd=0 (sto automatski daje 0 u odgovoru), treci slucaj kd=0.3 I =1.
domagojj
batman3000 Aha evo ispravak. @Tootha je dobro ukazao. prvo treba naci RBG koeficijente po formuli:
R=1-C
G=1-M
B=1-Y
knjiga strana 353.
pa tek onda uvrstavat u formulu jedan po jedan.
Tootha
VolimStopala🇻🇦🇭🇷 Ne bi li trebalo kd-ove za CMY pretvoriti u kd-ove za RGB i tek onda računati ovako kako si rekao?
domagojj
Tootha Kako se to radi? Nisam nigdje u slajdovima nasao primjer takve konverzije
Bica
Zna netko ovaj?

domagojj
Bica Nemam pojma, ako netko zna nek stavi
JoKing
ne znam jel točno rješenje. Al uglavnom imaš ove vrhove zadane (V), imaš centar C, ravnina projekcije je je z=0 (xy ravnina).
kad imaš zadane te vrijednost možeš računati točke koje nastaju nakon projekcije na ravnini. To računaš tako da prvo izračunaš pravac koji prolazi kroz centar projekcije i svaki od vrhova. Znači npr za CV1 dobiješ
[t, 1][[1, 2, -4, 0]
[0, 0, 6, 1]].
Kad si izračunao sve te pravce onda trebaš izračunati točke u kojima ti pravci sijeku ravninu. To napraviš tako da uvrstiš jednadžbu pravca (ovu gore) u jednadžbu ravnine (z=0). Kad to napraviš za prvu točku dobiješ -4t=-6 => t=3/2. Kad imaš t onda uvrstiš taj t u jednadžbu pravca da dobiješ (x,y,z) točke projekcije. Za prvu točku je to (3/2, 3, 0). Isti postupak napraviš i za sve ostale točke (rješenja su (3/2, 0, 0), (12/5, 12/5, 0)).
Sad imaš te točke i onda za točku računaš baricentrične koordinate pomoću sljedećeg sustava:
3/2*t1+3/2*t2+12/5*t3=2
3*t1+12/5*t3=2
t1+t2+t3=1.
Iz tog sustava dobiješ sljedeća rješenja:
t1=2/9 t2=2/9 t3=5/9.
Sada imaš vrijednosti koje se koriste u interpolaciji. Formula za interpolaciju izgleda
t1(0, 0) + t1(1, 1) + t2(0,1).
Kad uvrstiš vrijednost konačni rezultat ti je
(2/9, 7/9), odnosno (0.22, 0.78) što je odgovor c
bodilyfluids
VolimStopala🇻🇦🇭🇷 koji je link tih zadataka? ferko -> katalog zadataka mi otvara prazan frame