[AIPR] Gradivo
PrisonMike
M̵̧̩͑̀͝î̶͍̉ć̴̝̾́̀o̶̺̟̣͂̽ mislio sam zapravo na ovaj drugi dio kad minimiziramo po lambdi jer ulazi pod kvadrate, al da uz kalkulator se i to brzo riješi
PrisonMike
Murin kolko ti ispadnu početna točka i lambda na kraju?
Murin
Moguce da sam fulao jer sam nabrzaka racunao al ispadne mi X0=(3.5,3.2), a lambda ispadne -0.3095
i onda bi samo bilo xi=xi-lambda*parc_der_xi,dobijes novu tocku i preko toga se opet racuna novi smjer
johndoe12
kod box algoritma, kad racunam centorid, a imam dvije tocke s jednako losom f(x).. koju izaberem kao xh? i dal onda pri racuannju centroida izuzmem obe ili samo onu koja je xh?
micho
enaiks Isto kao i kod simpleksa se jedna od njih odredi kao gora
umjesto da gledaš na točke kao x_h i x_l, gledaj na njih kao x[-1] i x[0] u sortiranom nizu (po vrijednosti).
A zašto ne obje? Zato što si tako
- stvaraš nekvalitetniji centroid
- potencijalno ubiješ sve točke (zamisli da imaš samo 2: ukloniš obje i nemaš ništa)
Inače bi bilo sasvim logično maknuti obje, jer razlog zašto uopće mičemo te najlošije točke je samo zato da dobijemo malo bolju procjenu gdje se minimum nalazi pa bi onda htjeli da ni jedna ni druga ne utječe na centroid, ali to ne radimo da si ne sjebemo dalje algoritam. A koliko mi je poznato računanje centroida u Boxovom postupku je identično onome u Nelder Mead simpleksu.
johndoe12

b) to je visemodalni problem, jer sad imamo dva minimuma? jedan u (1, 2) a drugi u (3, 1.5)?
A konvergirat ce u tocku 4, 0.5 jer ima najmanju f(x)?
Stark
enaiks Kako odredim koliko lokalnih minimuma ima? A što se tiče konvergencije kod Boxa, pa valjda u jedan od tih minimuma?
koBASA
Murin
Mislim da cak nije bitna pocetna tocka, ionako je iduci smjer okomit
micho
Stark Kako odredim koliko lokalnih minimuma ima?
Najlakše ti je nacrtati
u ovom slučaju su ti sva ograničenja il neki rangovi brojeva, ili nešto iznad/ispod krivulje, ili unutrašnjost/vanjština neke elipse, da se
glider

kako bi izgledao postupak za ovaj?
koBASA
toblerone
Odma na pocetku videa
member
dammitimmad kako to? ja dobijem x2=2.337 (1.iter delta x = 2, x1=3, 2.iter delta x = -0.663
Noggenfogger
member u drugoj iteraciji sam slucajno GtG umjeto JtJ racunala. tocno ti je vjerojatno 🙂
Cereal_Killer
temari jesi uspio rjesiti? moze postupak? jako me zbunjuje a)
Noggenfogger
vagab0nd0
ja sam ovako, nisam sigurna u tocnost
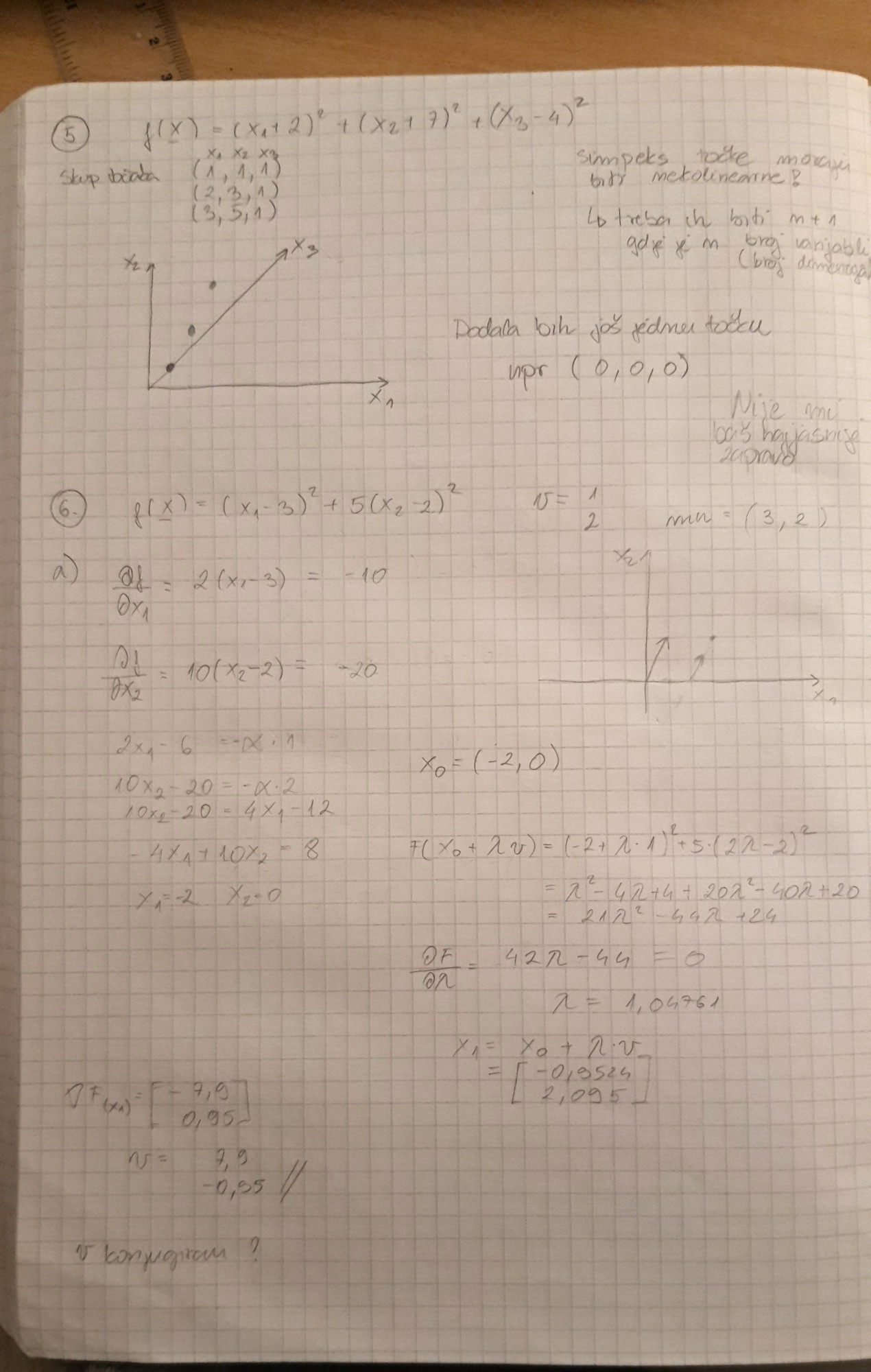

Murin
Nije mi jasno kako si dobila pocetnu tocku, tj od kud ovaj sustav
johndoe12
za v konjugirani nema jedinstvenog rjesenja jel?
Joji
- a) Gradijent u sljedećoj iteraciji bi trebo samo bit okomit vektor na ovaj koji je zadan jer se radi o gradijentom spustu na kvadratnoj funkciji, znači npr. \textbf v_{i+1} = [-2\quad 1]^\top. source: predavanje 05 2. sat oko 27:30
sphera
jel ima itko rješenja ispita iz 2019. da se može iskontrolirat?
member
dammitimmad hmm, ograničenja fja gi(x) bi trebala bit zadana kao gi(x)>=0, a ograničenja fja hj kao hj(x)=0. i uz to šta si napisala, mislim da bi trebalo odstranjivanjem eksplicitnog ograničenja dobit i novo ograničenje h(y) (npr 1+12sin**2(y)