Studoši

dinoo ono sto mi pada na pamet je da kad gledas po definiciji F(x,y) = P(X < x, Y < y), u svim tockama je ili 0 ili 1, ove tocke za koje je P(X < x, Y < y) = 1 znaci da je vjerojatnost 1 da je slucajna varijabla poprimila vrijednosti strogo manje od tih zadanih u (x,y), tako za svaku tocku (x,y) za koju je P=1 se spustas jer je poprimljena vrijednost strogo manja, sve dok odjednom naglo ne dode do tocke za koju je P=0, dakle nju ne moze isto poprimit a ne moze ni jednu manju od nje, po definiciji

drugim rijecima, u funkciji razdiobe, izmedu poprimanja vrijednosti 0 i 1 uvijek mora postojat jos neka vrijednost koju vjerojatnost poprima, to jer je F(x) = P(X < x) a ne = P(X <= x)
(ako se ne varam)

Rok ove godine. Jel moze neko objasnit otkud ovaj dokaz pod b)?

Kuhar Zero

Iskreno da vam kažem, trebalo mi je otprilike 2 sata gledanja u ovo rješenje da bih shvatio na koji način su oni to riješili, pa ću vam cijeli postupak isprezentirati od početka do kraja.

Ok, znači znamo da su X i Y nezavisne slučajne varijable sa istom, eksponencijalnom razdiobom sa parametrom \lambda = 1. Iz toga odmah možemo saznati njihove funckije gustoće f_X\left(x\right), f_Y\left(y\right) i funkcije distribucije (koje će nam trebati kasnije) F_X\left(x\right), F_Y\left(y\right).

Općenito, nevezano za zadatak, ako je X neka eksponencijalna slučajna varijabla sa parametrom \lambda > 0, odnosno
X \sim \mathscr{E}\left(\lambda\right)
tada su njene funkcije gustoće f_X\left(x\right) i distribucije F_X\left(x\right):
f_X\left(x\right) = \begin{cases} \lambda e^{-\lambda x} & \text{za} \ x > 0 \\ 0 & \text{inače} \\ \end{cases}

F_X\left(x\right) = \begin{cases} 1 - e^{-\lambda x} & \text{za} \ x > 0 \\ 0 & \text{inače} \end{cases}

ovo zadnje se izvede iz prvog jednostavnim integralom F_X\left(x\right) = \int_{-\infty}^{x} f_X\left(u\right) \mathrm{d}u po definiciji u slučaju da zaboravite.

U našem slučaju:
f_X\left(x\right) = \begin{cases} e^{-x} & \text{za} \ x > 0 \\ 0 & \text{inače} \\ \end{cases} \qquad f_Y\left(y\right) = \begin{cases} e^{-y} & \text{za} \ y > 0 \\ 0 & \text{inače} \\ \end{cases}

F_X\left(x\right) = \begin{cases} 1 - e^{-x} & \text{za} \ x > 0 \\ 0 & \text{inače} \end{cases} \qquad F_Y\left(y\right) = \begin{cases} 1 - e^{-y} & \text{za} \ y > 0 \\ 0 & \text{inače} \end{cases}

Okej, sad se pitamo sljedeće:
Dobro, ja sad znam kakve razdiobe imaju X i Y, ali na koju jebenu foru da znam (dobro aj znam da je uniformna, ali kako da dokažem) kakvu razdiobu ima slučajna varijabla Z = \frac{X}{X+Y} ?
Well odgovor ćemo naći ako pokušamo naći njenu funkciju distribucije F_Z\left(z\right) koju računamo po definiciji:
F_Z\left(z\right) = P \left(Z < z\right)
Interpretacija: koja je vjerojatnost da moja slučajna varijabla Z (veliko slovo, što znači slučajna varijabla) poprimi vrijednost manju od nekog odabranog broja z (malo slovo, što znači argument funkcije, odnosno nešto što pretpostavljamo da nam je poznato unaprijed, unlike slučajna varijabla koja nije poznata unaprijed) ?
Vještim manevriranjem dolazimo do sljedećeg:
F_Z\left(z\right) = P \left(Z < z\right) = P \left(\frac{X}{X + Y} < z\right) \newline \qquad = P \left(X < z\left(X + Y\right)\right) = P \left(X < zX + zY\right) = P \left(zY > X - zX\right) \newline \qquad = P \left(Y > \frac{1 - z}{z} X\right)

E sad ovdje morate paziti da ne šamarate te nejednakosti kako se vama sprdne. Ovdje smo koristili činjenicu da slučajne varijable X i Y mogu poprimiti isključivo strogo pozitivne vrijednosti (kad smo množili nejednakost sa X + Y da znak nejednakosti ostane isti), a u zadnjem koraku smo odlučili razmatrati slučaj samo ako je argument z strogo pozitivan, da opet znak nejednakosti ostane kakav je bio. Slučaj koji nismo time pokrili, z \leq 0 ćemo razmotriti kasnije.

I sad su se oni odlučili za jedan epski gamer move i koristili su formulu iz Elezovićevog udžbenika ViS Slučajne varijable: dno stranice 70, formula 7.3 koja kaže:

Ako ja imam neki događaj A čija vjerojatnost P \left(A\right) mi ovisi o tome kakvu vrijednost će poprimiti slučajna varijabla X, tada takvu vjerojatnost mogu računati tako da prvo nađem uvjetnu vjerojatnost P \left(A \mid X = x\right): vjerojatnost tog istog događaja A ako ja unaprijed znam koliku vrijednost će mi slučajna varijabla X poprimiti (to je ovaj dio “\mid X = x”), što je obično lakši posao. E onda kad sam našao tu uvjetnu vjerojatnost, i znam funkciju gustoće slučajne varijable X, e onda mogu zveknut ovakav integral:
P \left(A\right) = \int_{-\infty}^{+\infty} P \left(A \mid X = x\right) f_X\left(x\right) \mathrm{d}x
s tim da se ove granice integracije ravnaju prema tome kako i gdje je definirana funkcija gustoće f_X\left(x\right).

U našem slučaju, naš događaj A iz formule koji ovisi o tome kakvu vrijednost će poprimiti X je upravo događaj Y > \frac{1 - z}{z} X. Nas zanima P \left(Y > \frac{1 - z}{z} X\right), e al kada bismo znali koliko točno iznosi slučajna varijabla X i rekli neka je on jednak malom x(onaj dioX = x), e onda bi se takva vjerojatnost (sada uvjetna, P \left(Y > \frac{1 - z}{z} X \mid X = x\right), odnosno P \left(Y > \frac{1 - z}{z} x\right)) lako računala jer je s desne strane nejednakosti sada neki realan broj, a to možemo lako računati koristeći funkciju distribucije F_Y \left(y\right).

Nastavimo dalje gdje smo stali:

F_Z\left(z\right) = P \left(Y > \frac{1 - z}{z} X\right) \newline \qquad = \int_{-\infty}^{+\infty} P \left(Y > \frac{1 - z}{z} x\right) f_X\left(x\right) \mathrm{d}x
Zbog toga što funkcija gustoće f_X\left(x\right) nije nula samo za pozitivne x, granice integracije promijenimo u od 0 do +\infty. Uz to, vrijedi i sljedeće: P \left(Y > \frac{1 - z}{z} x\right) = 1 - P \left(Y < \frac{1 - z}{z} x\right) = 1 - F_Y \left(\frac{1 - z}{z} x\right). Tu smo koristili činjenicu da je Y kontinuirana slučajna varijabla (vjerojatnost događaja jednakosti je 0) i iskoristili smo definiciju funkcije razdiobe.

F_Z\left(z\right) = P \left(Y > \frac{1 - z}{z} X\right) \newline \qquad = \int_{-\infty}^{+\infty} P \left(Y > \frac{1 - z}{z} x\right) f_X\left(x\right) \mathrm{d}x \newline \qquad = \int_{0}^{+\infty} \left(1 - F_Y \left(\frac{1 - z}{z} x\right)\right) e^{-x} \mathrm{d}x

Sad moramo pravilno evaluirati F_Y \left(\frac{1 - z}{z} x\right). Ako se sjetimo kako izgleda funkcija razdiobe F_Y \left(y\right) naše eksponencijalne varijable Y, onda ćemo zaključiti da funkcija nije nula samo za pozitivne argumente. Dakle promatramo argument \frac{1 - z}{z} x i gledamo njegov predznak. Za početak, znamo da smo u domeni integracije pozitivnih x pa se za to ne trebamo brinuti. Ostaje nam gledati predznak izraza \frac{1 - z}{z}. Srednjoškolskim manevriranjem ovakvog trivijalnog pitanja zaključujemo da će biti strogo pozitivno ukoliko je 0 < z < 1. U tom slučaju možemo sa sigurnošću tvrditi da je F_Y \left(\frac{1 - z}{z} x\right) = 1 - e^{-\frac{1 - z}{z} x}, iz čega slijedi jedan od slučajeva:

F_Z\left(z\right) = \int_{0}^{+\infty} \left(1 - \left(1 - e^{-\frac{1 - z}{z} x}\right)\right) e^{-x} \mathrm{d}x \newline \qquad = \int_{0}^{+\infty} e^{-x \left(\frac{1 - z}{z} + 1\right)} \mathrm{d}x \newline \qquad = \int_{0}^{+\infty} e^{-\frac{x}{z}} \mathrm{d}x = -z e^{-\frac{x}{z}} \biggr|_{x=0}^{x \to +\infty} \newline \qquad = z \qquad \text{za} \ 0 < z < 1

A sad ako z nije iz tog intervala (ali opet unutar onog našeg na početku gdje smo manevrirali sa nejednakostima i rekli da ćemo slučaj z \leq 0 razmatrati kasnije jer tada ne zadržavamo isti znak nejednakosti), odnosno ako je z \geq 1 onda znamo da je cijeli izraz \frac{1 - z}{z} x negativan (ili 0), stoga će vrijediti F_Y \left(\frac{1 - z}{z} x\right) = 0.
Tada imamo još jedan slučaj:

F_Z\left(z\right) = \int_{0}^{+\infty} \left(1 - \left(1 - 0\right)\right) e^{-x} \mathrm{d}x = \int_{0}^{+\infty} e^{-x} \mathrm{d}x = 1 \qquad \text{za} \ z \geq 1

Sad napokon idemo razmotriti onaj slučaj, što ako je z \leq 0?
Da bismo dobili odgovor na to, vratimo se nazad na početak raspisivanja funkcije razdiobe F_Z \left(z\right):

F_Z\left(z\right) = P \left(Z < z\right) = P \left(\frac{X}{X + Y} < z\right)

I zapitajmo se, kolika je vjerojatnost, je li to uopće moguće, da izraz s lijeve strane nejednakosti \frac{X}{X + Y} bude manji od nečeg što je 0 ili strogo negativno (z) ? Pa naravno da ne, jer eksponencijalne slučajne varijable X i Y mogu poprimiti samo strogo pozitivne vrijednosti, stoga će i \frac{X}{X + Y} uvijek biti isključivo strogo pozitivan. Dakle ta vjerojatnost je 0.

F_Z\left(z\right) = P \left(Z < z\right) = P \left(\frac{X}{X + Y} < z\right) = 0 \qquad \text{za} \ z \leq 0

I onda naša funkcija razdiobe F_Z\left(z\right) u konačnici izgleda ovako:

F_Z \left(z\right) = \begin{cases} z & \text{za} \ 0 < z < 1 \\ 1 & \text{za} \ z \geq 1 \\ 0 & \text{za} \ z \leq 0 \end{cases}

Čak nije ni bitno gdje je jednakost a gdje nije jer u svakom slučaju je funkcija neprekidna.
I je li to stvarno liči na slučajnu varijablu uniformne razdiobe, odnosno je ii Z \sim \mathscr{U}(0, 1) ? Pa jest, u to se dodatno možemo uvjeriti ako deriviranjem funkcije razdiobe izračunamo funkciju gustoće f_Z \left(z\right) = \frac{\mathrm{d} F_Z}{\mathrm{d}z} \left(z\right)

f_Z \left(z\right) = \begin{cases} 1 & \text{za} \ 0 < z < 1 \\ 0 & \text{inače} \end{cases}

Sad ovakav način i onakvu formulu ja iskreno ne bih nikad iskoristio, jer samo komplicira stvari, a nema ništa lakše od good old šablone, koja je za ovakav tip zadataka naći gustoću vektora nezavisnih slučajnih varijabli: f_{X, Y} \left(x, y\right) = f_X \left(x\right) f_Y \left(y\right) (paziti na područja definiranosti) i onda vjerojatnost P \left(Y > \frac{1 - z}{z} X\right) računati dvostrukim integralom \int_{0}^{+\infty} \mathrm{d}x \int_{\frac{1 - z}{z} x}^{+\infty} f_{X, Y} \left(x, y\right)\mathrm{d}y. Doduše ovdje bi opet trebalo paziti na predznake i u kojem području integriramo ali opet lakše za shvatiti nego njihovo.

Zna li netko pod b)?

IdeGas Postoji mnogo načina za rješavanje ovakvih zadataka, ovako je najelegantnije:

10/10 crtež:

Ok znači slučajno odabiremo dvije točke nezavisno na dužini \overline{OA} i pri tome definirajmo slučajne varijable X_1 i X_2 kao njihove x koordinate. Čim se spominje odabiranje na sreću u nekom području, to odmah znači da se radi o uniformnoj (jednolikoj) razdiobi na tom području. Prema tome X_1, X_2 \sim \mathscr{U}\left(0, 1\right) i odmah znamo njihove funkcije razdiobe F_{X_k} \left(x\right) i funkcije gustoće f_{X_k} \left(x\right). U ovom rješenju će nam samo trebati funkcija razdiobe:
F_{X_k} \left(x\right) = \begin{cases} 0 & \text{za} \ x < 0 \\ x & \text{za} \ 0 \leq x \leq 1 \\ 1 & \text{za} \ x > 1 \end{cases}

Točka C je ona točka od onih dviju slučajno odabranih koja ima veću x koordinatu. Definirajmo novu slučajnu varijablu X_C koja će predstavljati x koordinatu točke C, dakle
X_C = \max{\{X_1, X_2\}}
Slučajna varijabla \Phi definirana je kao mjera kuta \angle OBC, i iz crteža je očito da je
\tan{\Phi} = X_C = \max{\{X_1, X_2\}} \newline \Phi = \arctan{\left(\max{\{X_1, X_2\}}\right)}

Ovaj zadnji korak smo mogli legalno napraviti (odnosno prilikom primjenjivanja funkcije arkus tangens na obje strane sa sigurnošću tvrditi da je \arctan{\left(\tan{\Phi}\right)} = \Phi ) zato što će naša slučajna varijabla \Phi biti sigurno unutar intervala \Phi \in [0, \frac{\pi}{4}], a u tom slučaju je funkcija tangens bijekcija pa se normalno može koristit njen inverz, arkus tangens.

Dobro, znamo kakvu distribuciju imaju X_1 i X_2 i pitanje je kako odrediti distribuciju od
\Phi = \arctan{\left(\max{\{X_1, X_2\}}\right)} ?
Well, opet možemo tražiti funkciju razdiobe F_{\Phi} \left(\varphi\right) iz definicije:
F_{\Phi} \left(\varphi\right) = P \left(\Phi < \varphi\right)

Odnosno tražiti vjerojatnost kada slučajna varijabla \Phi poprima manju vrijednost od zadanog argumenta funkcije \varphi
Za početak odmah možemo obraditi što se dešava ako kao argument \varphi uzmemo nešto izvan intervala [0, \frac{\pi}{4}]. Ako uzmemo argument \varphi > \frac{\pi}{4} logično da će događaj \Phi < \varphi uvijek desiti, a ako uzmemo \varphi < 0 onda se neće nikada desiti. Dakle zasad znamo one jednostavne slučajeve:
F_{\Phi} \left(\varphi\right) = \begin{cases} 0 & \text{za} \ \varphi < 0 \\ 1 & \text{za} \ \varphi > \frac{\pi}{4} \\ ... \end{cases}
Dobro, a sad idemo vidjeti što se desi ako se kao argument izabere \varphi \in [0, \frac{\pi}{4}]:
F_{\Phi} \left(\varphi\right) = P \left(\Phi < \varphi\right) = P \left(\arctan{\left(\max{\{X_1, X_2\}}\right)} < \varphi\right) = P \left(\max{\{X_1, X_2\}} < \tan{\varphi}\right)

U zadnjem koraku prilikom primjenjivanja funkcije tangens na obje strane nejednakosti, nejednakost neće promijeniti smjer iz razloga što je tangens rastuća bijekcija u slučaju koji mi promatramo.
Sad je pitanje, kako računati vjerojatnost da je maksimum nekog skupa manji od nekog broja (u našem slučaju \tan{\varphi})?
Pa ako je najveći broj nekog skupa manji, onda su i ostali u tom skupu.
F_{\Phi} \left(\varphi\right) = P \left(\max{\{X_1, X_2\}} < \tan{\varphi}\right) = P \left(X_1 < \tan{\varphi} \ , X_2 < \tan{\varphi}\right)
Ovaj zarez u sredini znači presjek dvaju događaja. Kako znamo da su varijable X_1 i X_2 nezavisne, gornji presjek možemo rastaviti na umnožak:
F_{\Phi} \left(\varphi\right) = P \left(X_1 < \tan{\varphi} \ , X_2 < \tan{\varphi}\right) = P \left(X_1 < \tan{\varphi}\right) \cdot P \left(X_2 < \tan{\varphi}\right)
A ove vjerojatnosti možemo lako računati koristeći funkcije razdiobe od X_1 i X_2:
F_{\Phi} \left(\varphi\right) = P \left(X_1 < \tan{\varphi}\right) \cdot P \left(X_2 < \tan{\varphi}\right) = F_{X_1} \left(\tan{\varphi}\right) \cdot F_{X_2} \left(\tan{\varphi}\right) = \left(F_{X_k} \left(\tan{\varphi}\right)\right)^2

Opet moramo paziti kako ćemo evaluirati tu funkciju sa argumentom \tan{\varphi}. Znamo da trenutno razmatramo slučaj 0 \leq \varphi \leq \frac{\pi}{4}, pa ako primijenimo funkciju tangens (opet imajući na umu da je to rastuća bijekcija) dobijemo
0 \leq \tan{\varphi} \leq 1 pa tada znamo u koji dio definicije funkcije razdiobe F_{X_k} \left(x\right) trebamo uvrstiti argument \tan{\varphi}:
F_{\Phi} \left(\varphi\right) = \left(F_{X_k} \left(\tan{\varphi}\right)\right)^2 = \tan^2{\varphi}
I ovime smo dovršili definiciju funkcije razdiobe F_{\Phi} \left(\varphi\right):
F_{\Phi} \left(\varphi\right) = \begin{cases} 0 & \text{za} \ \varphi < 0 \\ 1 & \text{za} \ \varphi > \frac{\pi}{4} \\ \tan^2{\varphi} & \text{za} \ 0 \leq \varphi \leq \frac{\pi}{4} \end{cases}
Zadatak nas traži da odredimo funkciju gustoće f_{\Phi} \left(\varphi\right), koju lako možemo dobiti deriviranjem funkcije razdiobe:
f_{\Phi} \left(\varphi\right) = \frac{\mathrm{d}F_{\Phi}}{\mathrm{d} \varphi} \left(\varphi\right)
f_{\Phi} \left(\varphi\right) = \begin{cases} \frac{2 \tan{\varphi}}{\cos^2{\varphi}} & \text{za} \ 0 \leq \varphi \leq \frac{\pi}{4} \\ 0 & \text{inače} \end{cases}
Pogledao sam službeno rješenje i ono je krivo jer njihovo rješenje ne zadovoljava osnovno svojstvo funkcije gustoće:
\int_{-\infty}^{+\infty} f_{\Phi} \left(\varphi\right) \mathrm{d} \varphi = 1.

Moje rješenje

Njihovo rješenje, lmao

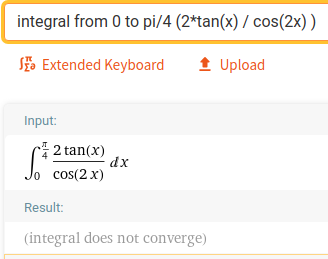
I još treba izračunati
P \left(\Phi > \frac{\pi}{6}\right) = 1 - P \left(\Phi < \frac{\pi}{6}\right) = 1 - F_{\Phi} \left(\frac{\pi}{6}\right) = 1 - \tan^2{\frac{\pi}{6}} = 1 - \frac{1}{3} = \frac{2}{3}

Da li smo mogli napisati doslovno samo rjesenja pod b) bez ovog izvoda? Jer u knjizici je jasno navedena formula za ishodisni moment eksponencijalne razdiobe viseg reda.

jel zna netko kako se mijenjaju parametri razdiobe u ovom i sličnim slučajevima? njihova rješenja su a) 0.7585 i b) 0.955. (ljir 2018.) ništa slično nisam našao ni u burićevim predavanjima ni u knjižicama. dobijam neka približna rješenja pa nisam siguran gdje griješim

caca
evo ako ti pomaže

zna li netko mozda ovo

light_grandma

Imaš identičan zadatak riješen u nekoliko redaka u Elezovićevom udžbeniku ViS Slučajne varijable na stranici 103.
Ja se takvog načina nikada ne bih sjetio, stoga sam odlučio detaljnije objasniti pristup kojim bih ja riješio taj zadatak.

Znamo da je X slučajna varijabla sa jediničnom normalnom razdiobom, odnosno
X \sim \mathscr{N} \left(0, 1\right)
i tada odmah automatski znamo kako izgleda njena funkcija gustoće f_X \left(x\right):
f_X \left(x\right) = \frac{1}{\sqrt{2 \pi}} e^{-\frac{1}{2}x^2} \quad \text{za} \ x \in \R
Nas zanima kakvu razdiobu ima slučajna varijabla Y = X^2, odnosno znamo da je gama razdioba, ali idemo to pokazati i uz to odrediti njene parametre.
U tu svrhu računat ćemo funkciju gustoće f_Y \left(y\right) koristeći formulu 5.1 na stranici 17 Elezovićevog udžbenika ViS Slučajne varijable. Kako koristiti tu formulu?
Dakle ta formula nam kaže ako znaš funkciju gustoće varijable X, kako računati funkciju gustoće f_Y \left(y\right)njene funkcijske transformacije Y = \Psi \left(X\right) (u našem slučaju to je obični kvadrat, \Psi \left(X\right) = X^2).

Za početak, formula zahtjeva da je transformacija \Psi injekcija (kasnije ću to zvati bijekcijom, surjekciju ću podrazumijevati). Već tu imamo problem, transformacija Y = X^2 nije bijekcija za sve realne X koje nam naša jedinična normalna slučajna može poprimiti. Stoga ćemo našu kvadratnu transformaciju podijeliti na dva bijektivna dijela: onda kad je X > 0 u prvom dijelu i onda kad je X < 0 u drugom dijelu. Razlog zašto je to bitno jest činjenica da se u ovoj formuli i cijelom postupku koristi inverz transformacije \Psi, odnosno \Psi ^{-1}, a inverz ne može postojati ako transformacija nije bijekcija. Dva slučaja znači da ćemo dobiti dvije funkcije gustoće od Y, f_{Y,1} \left(y\right) i f_{Y,2} \left(y\right) koje ćemo zbrojiti u područjima u kojima se preklapaju, bit će pojašnjeno kasnije.

Prvi dio: transformacija Y = X^2, \quad X > 0. Nađimo inverznu transformaciju (dakle transformacija oblika X = ...) jednostavnim korijenovanjem:
|X| = X =\sqrt{Y}, jer gledamo za X > 0 za apsolutnu vrijednost mogu samo maknuti
(sad ću prijeći na mala slova x i y)
Odredimo kud se transformacijom sve moguće vrijednosti x > 0 preslikaju u vrijednosti od y: \sqrt{y} > 0, odnosno
y > 0
Dalje, odredimo apsolutnu vrijednost derivaciju inverzne transformacije (u formuli apsolutna vrijednost \left|\frac{\mathrm{d} \Psi^{-1} (y)}{\mathrm{d}y}\right|, odnosno \left|\frac{\mathrm{d} x}{\mathrm{d}y}\right|)
U našem slučaju imamo
x = \sqrt{y}
\frac{\mathrm{d} x}{\mathrm{d}y} \left(y\right) = \frac{1}{2 \sqrt{y}}
\left|\frac{\mathrm{d} x}{\mathrm{d}y} \left(y\right)\right| = \left|\frac{1}{2 \sqrt{y}}\right| = \frac{1}{2 \sqrt{y}}

I onda napokon primijenimo danu formulu u knjizi (u funkciji gustoće od X, odnosno f_X \left(x\right) kao argument uvrstimo inverznu transformaciju):
f_{Y, 1} \left(y\right) = f_X \left(\sqrt{y}\right) \left|\frac{\mathrm{d} x}{\mathrm{d}y} \left(y\right)\right|
f_{Y, 2} \left(y\right) = \frac{1}{\sqrt{2 \pi}} e^{-\frac{1}{2}\left(\sqrt{y}\right)^2} \cdot \frac{1}{2 \sqrt{y}} = \frac{1}{2\sqrt{2 \pi}} \cdot \frac{1}{\sqrt{y}} e^{-\frac{1}{2}y} \qquad \text{za} \ y > 0

Sad napravimo isti postupak sa drugim bijektivnim dijelom naše transformacije:
Y = X^2, \quad X < 0
Inverzna transformacija (|X| sada pak prelazi u -X jer je X < 0):
|X| = -X = \sqrt{Y} \newline X = -\sqrt{Y}
Preslikavanje područja (kao i u prethodnom slučaju ispadne y > 0 pa će doći do preklapanja):
x < 0 \newline -\sqrt{y} < 0 \newline \sqrt{y} > 0 \newline y > 0
Apsolutna vrijednost derivacije inverza:
\left|\frac{\mathrm{d} x}{\mathrm{d}y} \left(y\right)\right| = \left|-\frac{1}{2 \sqrt{y}}\right| = \frac{1}{2 \sqrt{y}}
Te funkcija gustoće:
f_{Y, 2} \left(y\right) = f_X \left(-\sqrt{y}\right) \left|\frac{\mathrm{d} x}{\mathrm{d}y} \left(y\right)\right| = \frac{1}{\sqrt{2 \pi}} e^{-\frac{1}{2}\left(-\sqrt{y}\right)^2} \cdot \frac{1}{2 \sqrt{y}} = \frac{1}{2\sqrt{2 \pi}} \cdot \frac{1}{\sqrt{y}} e^{-\frac{1}{2}y} \qquad \text{za} \ y > 0

I sad gledamo preklapaju li se područja definicija funkcija f_{Y, 1} \left(y\right) i f_{Y, 2} \left(y\right)?
Odgovor je: da, u potpunosti kod y > 0. Onda ćemo ih u tom slučaju jednostavno zbrojiti (u općenitom slučaju zbrajamo dijelove funkcija koje se preklapaju):
f_Y \left(y\right) = f_{Y, 1} \left(y\right) + f_{Y, 2} \left(y\right)
Kako su identične u oba slučaja, efektivno množimo sa 2. Dodatan primjer takvog “zbrajanja” gustoći imate na primjeru 5.11 na stranici broj 18 u već spomenutom Elezovićevom udžbeniku. Naravno, nemojmo zaboraviti naš good old “0 inače” kojeg uvijek stavljam radi potpunosti definicije funkcije nad svim realnim brojevima.

f_Y \left(y\right) = \begin{cases} \frac{1}{\sqrt{2 \pi}} \cdot \frac{1}{\sqrt{y}} e^{-\frac{1}{2}y} & \text{za} \ y > 0 \\ 0 & \text{inače} \end{cases}

Dobro, našli smo funkciju gustoće od Y, no sad je pitanje, je li ona uistinu ima gama razdiobu, odnosno je li
Y \sim \mathscr{G} \left(\alpha, \lambda\right) ?
U zadatku nam je dano i kako izgleda funkcija gustoće gama razdiobe (ja ću ju označiti sa f_{\mathscr{G} \left(\alpha, \lambda\right)} \left(y\right)) s parametrima \alpha > 0,\ \lambda > 0 (kao argument sam stavio slovo y umjesto x radi boljeg uočavanja sličnosti sa funkcijom koju smo prethodno računali):
f_{\mathscr{G} \left(\alpha, \lambda\right)} \left(y\right) = \frac{\lambda^{\alpha}}{\Gamma \left(\alpha\right)} y^{\alpha - 1} e^{-\lambda y} \qquad \text{za} \ y > 0
Gdje je \Gamma \left(\alpha\right) gama funkcija definirana kao
\Gamma \left(\alpha\right) = \int_{0}^{+\infty} x^{\alpha - 1} e^{-x} \mathrm{d}x \qquad \text{za} \ \alpha > 0
Sad usporedimo strukturu naše funkcije gustoće f_{Y} \left(y\right) sa strukturom funkcije gustoće gama razdiobe f_{\mathscr{G} \left(\alpha, \lambda\right)} \left(y\right).
Gledajući eksponente potencija broja e možemo naslutiti da je \lambda = \frac{1}{2}, a ako pogledamo potenciju sa bazom y možemo naslutiti da je \alpha - 1 = -\frac{1}{2}, odnosno da je \alpha = \frac{1}{2}. Da bismo to potvrdili, moramo gledati konstantni faktor. Ako parametri \alpha i \lambda stvarno jesu jednaki \frac{1}{2}, tada bi se taj konstantni faktor u našoj funkciji gustoće morao moći preurediti da u brojniku piše \frac{1}{\sqrt{2}} što je \lambda^{\alpha}, a u nazivniku \sqrt{\pi}, odnosno \Gamma \left(\frac{1}{2}\right), što je \Gamma \left(\alpha\right).
Sad moraš biti bog i batina da se sjetiš nekih svojstva gama funkcije i činjenice da vrijedi \Gamma \left(\frac{1}{2}\right) = \sqrt{\pi}. To se izračuna integralom iz definicije gama funkcije pomoću ingeniozne supstitucije, pogledaj na stranici 100 u udžbeniku za više informacija o gama funkciji.

Zaista, naš konstantni faktor se može tako preurediti:
f_Y \left(y\right) = \frac{1}{\sqrt{2 \pi}} \cdot \frac{1}{\sqrt{y}} e^{-\frac{1}{2}y} = \frac{\frac{1}{\sqrt{2}}}{\sqrt{\pi}} y^{-\frac{1}{2}} e^{-\frac{1}{2}y} \qquad \text{za} \ y > 0

I ovime smo pokazali da naša slučajna varijabla Y stvarno ima gama razdiobu sa parametrima \alpha = \lambda = \frac{1}{2}, odnosno Y \sim \mathscr{G} \left(\frac{1}{2}, \frac{1}{2}\right).

Ima li tko rijesene ispite proslih godina pa da slika i stavi u 1 file i uploada ovdje…bio bih jako zahvalan 🙂

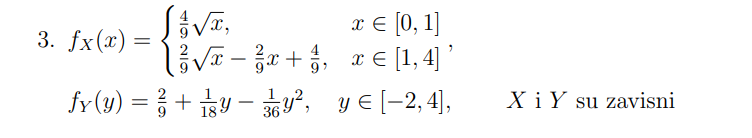
Kako ovdje dobit f(x,y). Oke znam da je jedinična ali sta uzmem za interval b-a? Koliko mogu iz rjesenja iscitat njima je f(x,y) = ⅑

Kuhar Općenito, za bilokoju dimenziju slučajnog vektora (znači u tvom primjeru radi se od slučajnom vektoru \left(X, Y\right) sa 2 komponente X i Y, a ovo što ću ti ja sad reći vrijedi za slučajne vektore \overrightarrow{X} = \left(X_1, X_2, ..., X_n\right) sa proizvoljno mnogo komponenata), ako taj slučajni vektor ima jednoliku razdiobu na području G, tada funkcija gustoće f_{\overrightarrow{X}} \left(\overrightarrow{x}\right) izgleda ovako (ovaj zapis \overrightarrow{x} promatraj kao višedimenzionalnu točku \left(x_1, x_2, ..., x_n\right), stavio sam tako samo radi kompaktnijeg zapisa):

f_{\overrightarrow{X}} \left(\overrightarrow{x}\right) = \begin{cases} \frac{1}{\operatorname{m} (G)} & \text{za} \ \overrightarrow{x} \in G \\ 0 & \text{za} \ \overrightarrow{x} \notin G \end{cases}

Gdje je \operatorname{m} (G) mjera područja G. U slučaju jedne dimenzije to je duljina (i to ti je ono b - a na što si mislio, to je duljina područja (intervala) kod jednodimenzionalne uniformno distribuirane slučajne varijable X \sim \mathscr{U} \left(a, b\right), pa zato gustoća u tom intervalu je \frac{1}{b - a}), u slučaju dvije dimenzije to je površina, a u slučaju 3 dimenzije to je volumen.
Kako ti imaš dvodimenzionalni slučajni vektor, ti moraš računati površinu. I kod tebe je područje čiju površinu računaš (famozno područje G) omeđeno krivuljama y^2 = 4x i y = 2x - 4. Kad skiciraš te krivulje lako računaš površinu, ili matan1 style jednostrukim integralom ili matan2 style dvostrukim integralom sa podintegralnom funkcijom 1 i proper granicama.
Ja preferiram dvostruki, i ovdje se može bez rastavljanja ako izabereš poredak po y pa onda po x. Ako ti nije jasno kako sam došao do tih granica, reci.
\operatorname{m} \left(G\right) = \int_{-2}^{4}\mathrm{d}y \int_{\frac{1}{4}y^2}^{\frac{1}{2}y+2} \mathrm{d}x = ... = 9
Prema tome, tvoja funkcija gustoće f_{\left(X,Y\right)} \left(x, y\right) slučajnog vektora izgleda ovako:
f_{\left(X,Y\right)} \left(x, y\right) = \begin{cases} \frac{1}{9} & \text{za} \ \left(x, y\right) \in G \\ 0 & \text{za} \ \left(x, y\right) \notin G \end{cases}

Kuhar Ovo bih ti rado pomogao da sam to testiranje hipoteza actually naučio

Jel njima ovo rjesenje skroz krivo ili ja zujim? Cini mi se ko da su i kvantil krivo ocitali? ZI-18.

Kuhar
očito si negdje fulao

tomekbeli420
Hvala puno legenda si

koji kurac je vlakic na svakom grafu s buricevih predavanja za slucajne vektore

Ekipa ikakva očekivanja za sutra, malo nas je prijavilo pa sam čuo da bi ga mogli zapapriti?

Mrnjotaur Ljetni i zimski rok su bili gadni tak da se nadam da ce se malo smilovati ovog puta, mozda ubace i statistiku 😅

light_grandma
Alfa * 2 jer su u pitanju dvije populacije?