[VIS] Pitanja i odgovori
Tompa007
endyyyy ajde hvala ti puno , već ga 7 put raspisujem , jesi to na VIS uplodala jer ne mogu naci nazalost ? :/
AK10
𝐓𝐇𝐄 𝐒𝐄𝐂𝐑𝐄𝐓 - 𝐂𝐋𝐔𝐁 ma nemam ti ja pojma kako se to ispravno stavi na ove materijale, ako ti se ne da cekati da mićo reagira javi se pa cu ti na mail poslati il nekako vec
Aloko

ne mogu se sjetiti kad se tocno koristi ovo zbrajanje i oduzimanje s 0.5 kako bi se povecala tocnost rezultata, a sjecam se da je jednom @Pineo to objasnio. Jel se neko zna mozda?
Pineo
Ardeo tldr; ne morate o tome razmišljat niti raditi tu korekciju 0.5
niknik
Pineo FER2 program sam, ostao mi je VIS za jesen. Ako ga ne prođem upisujem ga sljedeće godine u zimskom semestru po FER3 programu i nosi 6 ECTS-a. U aplikaciji za upis uz obavezne predmete za 5. semestar + VIS zbroj ectsa mi je 38. Trebam li onda to tako ostaviti i samo predati molbu za upis više od 37 ECTS-a u studentsku službu ili?
KR7


Jel moze neka dobra dusa rijesit ovaj zadatak, u rjesenjima nema postupka samo konacno rjesenje. 😒
Krisle
Mislite da će doći kakav zadatak iz 8. knjizice? Nisam ih baš susretao na ispitima
Upforpslone
od kud njima u a) f(y) ?

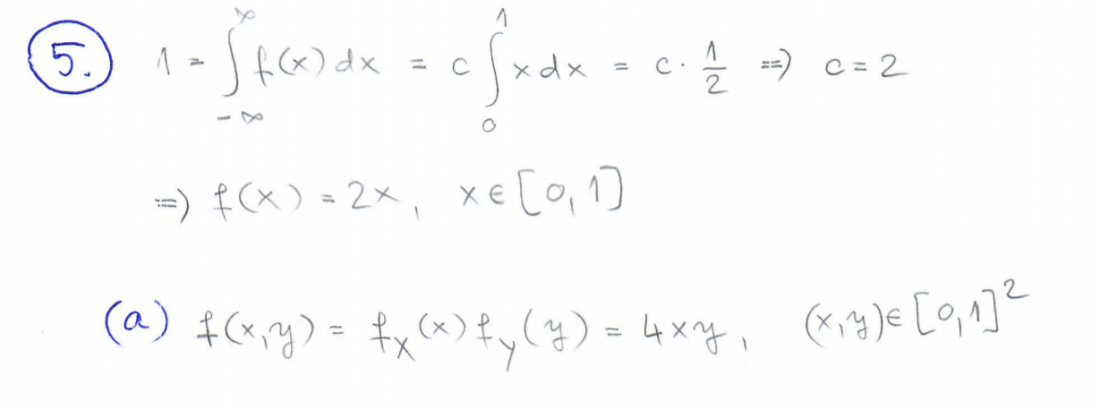
[obrisani korisnik]
Upforpslone Piše ti da je taj graf funkcije gustoće i za X i za Y.
Jest da gore u grafu piše f(x), ali taj x je samo oznaka varijable, tu je moglo pisati u i f(u).
Aquaman
ima li itko informacije kako ce biti rasporedeno gradivo po zadacima s obzirom da ce biti 6 zadataka. Meni se to cini nekako mal broj zadataka da bi pokrili sve. Takodjer, znaci li to da ce zadaci biti skalirani tako da svaki nosi 13.33 bodova. 😉
Tompa007
Aquaman 90 je max bodova , 10 * 1.5 * 6 , svaki zdatak = 15 bodova
zplusplus
Aquaman nez jesi fer2 ili fer3, na fer2 ispit obično nosi 50 i svake godine je drugačije raspoređeno po zadacima, a onda se ostvareni broj od tih 50 množi sa (2) ili (1.6 + KPZ)
Aquaman
𝐓𝐇𝐄 𝐒𝐄𝐂𝐑𝐄𝐓 - 𝐂𝐋𝐔𝐁 kako 90 ako kpz nosi 20
Aquaman
gasaf fer2 sam, al cini mi se da ce biti 6 zadataka jer je tako na obrascu za koji su nam rekli da ce nam dati prilikom rjesavanja. Mislio sam ako je netko bio na konzultacijama pa ima neke informacije na sto ce se vise bazirati.
PeanutMaster1801
Aquaman na fer3 kpz nosi 10
Tompa007

ima neko ovaj 10 mozda ?
Tompa007
𝐓𝐇𝐄 𝐒𝐄𝐂𝐑𝐄𝐓 - 𝐂𝐋𝐔𝐁 
u slicnom zadatku kod profesora Burića je rijesen ovaj zadatak gdje su za n i m uzeli broj dana, dok u ovom zadatku na ispitu ne uzmu broj mogucih ocjena (2,3,4,5)=4 , nego zbroj svih ocjena , pa me zanima kako se odreduje ovaj n i m kod hipoteze o jednakosti nezavisnih normalnih varijablu s nepoznatom disperijom
angello2
𝐓𝐇𝐄 𝐒𝐄𝐂𝐑𝐄𝐓 - 𝐂𝐋𝐔𝐁 ovo je wild guess al da nije mozda zato kaj u zadatku s ocjenama pita za prosjek (očekivanje) svih ocjena, dok u ducanu pita za prosjek (očekivanje) po jednom danu a ne u cijelom tjednu? nez jel to ima smisla
Erpeg

Jel moze neko objasnit zasto u prvom zadatku ide samo e^-lambdaX, a u drugom ide 1- …
Ima li opcenito definirano kada ide 1- a kada ide samo e^-lambdaX
AK10
Erpeg
P(X<n) = F(n) = 1 -e -λx
P(X>n) = 1 - P(X<n) = 1-( 1-e -λx )=e -λx
tomekbeli420
Erpeg
Ista stvar dobivena na drugi način, svejedno koji način ćeš iskoristiti (nevezano za zadatak).
Prvi način je korištenjem funkcije gustoće. Naime, znamo da eksponencijalna slučajna varijabla X \sim \mathscr{E} \left(\lambda\right) ima funkciju gustoće f_{X}\left(x\right) = \lambda e^{-\lambda x}
Recimo za neki poznati broj a \geq 0, kako računati vjerojatnost P \left(X > a\right) ?
Sa funkcijom gustoće to se računa njenim integriranjem:
P \left(X > a\right) = \int_{a}^{+\infty} f_{X} \left(x\right) \mathrm{d}x \\
P \left(X > a\right) = \int_{a}^{+\infty} \lambda e^{-\lambda x} \mathrm{d}x
Uvođenjem supstitucije u = e^{-\lambda x} \quad \mathrm{d}u = -\lambda e^{-\lambda x} \mathrm{d}x gornji integral se svodi na
P \left(X > a\right) = \int_{e^{-\lambda a}}^{0} - \mathrm{d}u = - u \biggr|_{e^{-\lambda a}}^{0} \\
P \left(X > a\right) = e^{-\lambda a}
Drugi način je korištenjem funkcije distribucije F_{X} \left(x\right), a za eksponencijalnu slučajnu varijablu znamo da je F_{X} \left(x\right) = 1 - e^{-\lambda x} (što se izvede sličnim integralom jer je funkcija gustoće derivacija funkcije distribucije).
Po definiciji funkcije distribucije vrijedi:
P \left(X < a\right) = F_{X} \left(a\right) \\
1 - P \left(X > a\right) = F_{X} \left(a\right) \\
P \left(X > a\right) = 1 - F_{X} \left(a\right) = 1 - \left(1 - e^{-\lambda a}\right) \\
P \left(X > a\right) = e^{-\lambda a}
Tak da ti je svejedno kako ćeš računati takve vjetojatnosti.