Studoši

Ako mi netko može samo objasniti logiku ZZV 3.25 i sličnih zadataka bio bi zahvalan:

U zadatku kaže da se traži vjv. ispravnog dekodiranja slijeda bitova x, ali nije navedeno koliko je taj slijed dugačak - može biti 7 bitova, može biti 7000. E sad, ja znam kak se rješavaju ti zadaci, tako da se kodira samo prvi slijed bitova koji stane u koder i za njega se izračuna vjv. ispravnog dekodiranja i to je rješenje za cijeli slijed x. No moje pitanje je zašto to vrijedi za cijeli slijed x, koji (u teoriji) može imati milijune i milijune bitova?

Ako npr. dobijemo da je vjv. ispravnog dekodiranja prvog slijeda bitova 0.98, kako možemo onda zaključiti da je vjv. ispravnog dekodiranja cijelog slijeda x također 0.98 (što je ispravno rješenje)? Zar nije logičnije po nekom VIS-u da ako je vjv. ispravnog dekodiranja prvog slijeda 0.98 i imamo 10 slijedova u nizu x, vjv. ispravnog dekodiranja 0.98¹⁰, jer se svaki slijed mora ispravno dekodirati da bi cijeli niz x bio u potpunosti dobro dekodiran?

Bio bi jako zahvalan ako bi mi netko ovo mogao objasniti, nije mi nužno za rješavanje zadataka al bi volio skužiti i koncept a ne samo naštrebati postupak.

Zadatak 1.10 iz zbirke (neriješeni zadaci),

zna li ga možda netko malo pojasniti?

Nisam shvatila je li alfa vjerojatnost da X poprimi vrijednost iz skupa X1 ili je alfa vjerojatnost pojavljivanja svakog simbola unutar skupa X1?

Emma63194 S obzirom na to da ti suma vjerojatnosti pojavljivanja simbola mora biti 1, onda \alpha može jedino biti vjerojatnost da X poprimi vrijednost iz Skup_1. X_1 i X_2 nisu skupovi, već diskretne slučajne varijable, ovo je bitno jer razdioba vjerojatnosti u njima nije nužno uniformna.

Zadatak je običan skup particioniran na 2 podskupa iz kojih se uzorkuje s određenom vjerojatnosti. Rješenje je H(X) koji ovisi o navedenim varijablama. Kao hint, prvo bi bilo dobro napraviti H(X) neovisan o \alpha. Onda će biti lako vidjeti da je \alpha najobičniji parametar težina.

M̵̧̩͑̀͝î̶͍̉ć̴̝̾́̀o̶̺̟̣͂̽ Hvala na odgovoru i objašnjenju!
Što se hinta tiče, nisam sigurna kako to raspisati bez parametra alfa.

Moj pokušaj rješavanja zadatka je bio ovo:

no ne znam kako ovim pristupom dobiti ovaj zaokruženi dio iz rješenja.

Emma63194

Krivo si postavila formulu. Kaze da je s vjerojatnostcu \alpha X poprima vrijednost slucajne varijable X_1, a s 1-\alpha vrijednost slucajne varijable X_2.

No X_1 i X_2 su slucajne varijable koje imaju svoje razdiobe. I sad ti iz ovoga moras prvo odrediti razdiobu slucajne varijable X. Neka je sada i = 1, \ldots m . Ako imas da je X = X_1 , onda je uvjetno na to vjerojatnost da X poprimi i jednaka vjerojatnosti da je X_1 = i odnosno p_i . A vjerojatnost da X poprimi vrijednost iz X_1 je \alpha . A ako je X_2 “jednak” X onda je uvjetno na to vjerojatnost 0 (jer je X_2 poprima samo vrijednosti vece od m. Dakle za i = 1, \ldots, m imamo:
P(X = i) = \alpha \cdot p_i + (1-\alpha)\cdot 0 = \alpha \cdot p_i
Analogno za i = m+1, \ldots, m+n imas:
P(X= i ) = \alpha \cdot 0 + (1 - \alpha) \cdot p_i = (1 - \alpha) \cdot p_i

Dakle sveukupno:
P(X = i ) = \begin{cases} \alpha p_i, & 1 \leq i \leq m \\ (1-\alpha)p_i, & m + 1 \leq i \leq m+n \end{cases}

I sade s tim vjerojatnostima racunas entropiju H(X) (dakle uvrstis ih i u logaritam, i odna koristist pravilo da je logartima umnoska zbroj logaritama, malo to raspises i preoznas gdje je H(X_1) i H(X_2) i trebala bi dobiti na kraju trazeno.).

Dakle u osnovi ovdje treba shvatiti razmisljanje ovako, prvo s vjerojatnoscu \alpha biramo vrijednosti slucajne varijable X_1 i onda s vjerojatnosti p_i biramo tu neku vrijednost i = 1, \ldots, m . Analogno i za vrijednosti X_2.

Ovdje se ne poklapaju vrijednosti od X_1 i X_2 pa mozemo ovako jednostavno po slucajevima, da se poklapaju ne bismo mogli nesto previse zakljuciti (jedino ako mozda znamo da su nezavisne ili sl., ali opet upitno).

riješeni primjeri, zadatak 2.18 LZ77 algoritam, zašto je u 3. koraku izlaz iz dekodera (1,4,b)? Je li ne bi trebalo biti (1,5,b) pošto b 5 puta matchamo s b u PP?

NISAM ASISTENT istina, ali trebaš imati na umu da uzmeš svih 5 slova b iz PZK, onda bi ti izlaz bio (1,5,c), jer si iskoristio svih 5 slova b iz PZK te je sljedeći znak nakon njih c. No, u tom slučaju sljedeći simbol bi ti bio c, a jedno od pravila kod kodiranja sa LZ77 je da sljedeći simbol uvijek mora biti iz PZK-a, a c to nije. Zato se ipak moraš zaustaviti jedno mjesto prije, da ti sljedeći znak također bude iz PZK-a, te stoga pišeš (1,4,b)

[obrisani korisnik]
EDIT: Dakle ovo gore rezoniranje ti je ustvari ovo:
P(X = i ) = P(X= i, X = X_1 \text{ili}\ X = X_2) = P(X=i, X = X_1) + P(X =i, X= X_2) = \\ =P(X=i | X=X_1) P(X=X_1) + P(X = i | X=X_2) P(X=X_2) = \\ =P(X_1 = i) P(X=X_1) + P(X_2=i) P(X=X_2)
Naime dogadaji \{X=X_1 \} i \{X = X_2\} su disjunktni (jer X_1 i X_2 poprimaju razlicite vrijednosti) pa onda vrijedi druga jednakost u prvom redu (vjerojatnost disjunktne unije je suma vjerojatnosti), a kako X poprima samo njihove vrijednosti onda vrijedi prva jednakost u prvom redu.

Jel vrijedi da je h(x) koda K generirajući polinom njegovog dualnog koda?

Mi koji nismo isli na ljetni rok sad imamo prakticki jos 3 roka ( ovaj novi dodatni, jesensk i dekanski)?

steker Da

Može li mi netko samo reći gdje griješim u primjeru 2.6? Treći put ga već riješavam i stalno dobivam krivo, a ne vidim gdje bi mogla biti greška

Moje rješenje

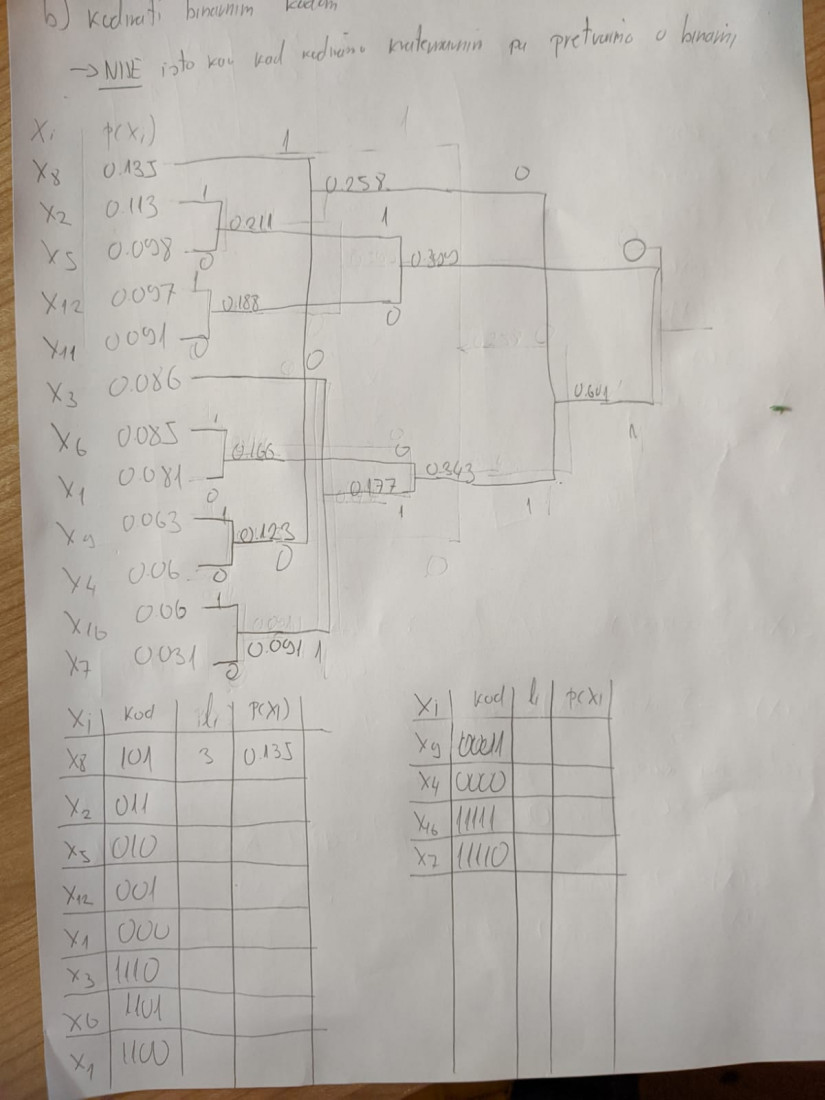
Njihovo rješenje

indythedog To je i mene mučilo, ali malo sam bolje pogledao i shvatio da su oni kombinirali x3 i x11 umjesto onoga što si ti x3 i (x10, x7) (pogledaj, oni imaju iste vjerojatnosti p(x10, x7) == p(x11)).

it_is_what_it_is Tnx, da u pravu si.
Ja sam mislio da kad imaš 2 simbola iste vjv. da uvijek biraš onaj niži u stablu, no sudeći po ovom valjda možeš koji god hm, možda je to zbog uvjeta da L(x) bude najmanji mogući

2.25 iz riješenih zadataka LZW algoritam, bi li mogao tko pojasniti na ovom primjeru kako dekodirati poruku uz početni rječnik?
kod: 1 2 3 5 4 1 8 2
p. rječnik 1=A, 2=B

Ja dođem do koraka gdje dobijem prva 4 simbola poruke, ali mi je dalje nejasno kako bi trebao dobiti što je vrijednost 5 iz rječnika.

bodNaUvidima evo da odgovorim sam sebi i nekom drugom ako zapne na istom pitanju, ovdje ima napisan algoritam za dekodiranje https://www.geeksforgeeks.org/lzw-lempel-ziv-welch-compression-technique/

bodNaUvidima
meni je ovaj tip fino pojasnio i sve sam zadatke rijesio iz prve tocno u zbirci. jednostavno napravis si tu tablicu i samo laganini.

Može netko pojasniti iz zbirke 3.35?
Ne razumijem šta od mene hoće, pogledao sam ono što je stavljeno na materijalima ali ne razumijem odkud mu da je d(x)=1, piše da je najmanja, ali prvi simbol je 0, šta onda ne bi trebalo biti d(x)=0???

it_is_what_it_is
Ovo je moje rješenje

Znači, prvo treba odrediti n tako da bude najmanji moguć. To određujemo uz pomoć činjenice da ako je g(x) generirajući polinom nekog koda koji ima duljine kodnih riječi n, onda xⁿ - 1 mora biti djeljivo sa g(x) bez ostatka. Očito je da nije 1,2 ili 3, 4 ne može biti jer g(x) nije dijeljiv sa x⁴ - 1, n nije ni 5 jer g(x) nije dijeljiv bez ostatka sa x⁵ - 1, no sa x⁶ - 1 je djeljiv, dakle n = 6. Znamo da je stupanj g(x) = 4, dakle r = 4, a iz formule k = n - r dobivamo da je k = 2.

Sad, pošto je k = 2, to znači da trebaš kodirati prva 2 simbola koja ti dolaze na ulaz kodera, dakle riječ koju trebaš kodirati je d = [01], odnosno 1 u polinomskom zapisu (jer 1 * x⁰ + 0 * x¹ = 1).

I sad kad imaš d u polinomskom zapisu (d(x) = 1), pomoću one klasične formule r(x) = d(x) * x^r mod[g(x)] računaš CRC, te se dobije x² + 1, odnosno 0101 kad pretvoriš u binarni zapis (0101 jer je r = 4 pa treba CRC zapisati sa 4 bita)

indythedog
Jaooo hvala ti. Znao sam da je s polinomima, no gledao sam na njihovoj prezentaciji faktorizaciju ali nigdje nisu spomenuli faktorizaciju x⁶+1, a nisam išao gledati po internetu postoji li. Hvalaa tiii