Studoši

Evo moja pitanja i odgovori s prvog moodle kviza. Imamo li svi ista pitanja ili su se nekome pojavila i druga?

Cvija Svi imamo ista pitanja.

Zašto ovdje d) nije isto točno?

Yeltneb ja mislim da ne mozes znat hoce li generalizrati bolje jer je sum u podacima velik, a ovo je vrlo jaka regularizacija

InCogNiTo124 pa baš zato što je šum velik bi d) trebao biti točan

kako se najbolje pripremiti za ispit, imajući na umu da je na zaokruživanje

Zna možda netko objasniti ovak zadatak?
Nisam sigurna kako su došli do tih težina, niti kako opće pristupiti zadatku.

Emma63194 ma taj je lagani kjut zadatak haha

Prvo krenimo od dataseta koji je generiran onom Gaussovom razdiobom, onaj izraz ti je pravac kojeg bi kao trebala dobit da ti je loss funkcija dobra, to je stvarni pravac

No, nemas dobru loss funkciju.
Doduse, fear not, jer ako se samo malo algebarski poigras, (y + h(x))² = (y - (-h(x))², odnosno, efektivno ucis nad podacima koji su flipani oko x osi.

(Alternativno, loss ti moze biti i (h(x) - (-y))² gdje se bolje vidi da y mjenja predznak. Razmisli zasto)

E sad ostavljam tebi za vjezbu da nades jednazbu pravca koji nastane flipanjem ovog zadanog u Gaussovoj oko x osi

Edit: nisam objasnio odakle tezine, pliz napravi korespondenciju izmedu tog kak ti izgleda hipoteza i kak ti izgleda pravac, i trebala bi moci matchat iz tog sta ti je w0 a sta w1

[obrisani korisnik]

InCogNiTo124

Daniel Plainview Ne, jer šum ti onemogućava generalizaciju. Zapamti, ti na šumu učiš. Ako je šum velik, uopće ne moraš točno učiti. A s obzirom na to da imaš istu dimenzionalnost, isto se prenauče, ovaj reguliziraniji se manje prenauči (iako s tim faktorom se vjv ni ništa ne nauči), ali za generalizaciju nemaš pojma.

Daniel Plainview da, samo zato sto je regularizacija velika ne znaci da model magicno dobro generalizira, veliki sum ti ubije sve

Koja je zadnja lekcija koja ulazi u ispit?

https://www.mentimeter.com/s/df70e13555085506b871dc515e4f44cb/ce9e776fe49b
https://www.mentimeter.com/s/38c974c6640c7520ad54fc83dd1f468b/e4860d794295
https://www.mentimeter.com/s/4b3a322d9a5f54d7fd253a02518ac220/e77cdb7938c2
https://www.mentimeter.com/s/f902613407ba3a6ab9778bde7b7d50e4/8262859a3f35
https://www.mentimeter.com/s/781be9192b1e81635b6f73c40854512e/df1436b7dddf
https://www.mentimeter.com/s/63d94575856c4b46e47284cd7f9eb3e3/9e974b9d4432
https://www.mentimeter.com/s/4e525c01d764d0b3eada097d627d86c9/1e95be59ccaa
https://www.mentimeter.com/s/c49df11f9b48e73acc50d814ef92148a/297af9dfbcf7
https://www.mentimeter.com/s/a2ed2615daff6262eb076b0e6004dd38/d886773799f1
https://www.mentimeter.com/s/5de36dbb4fb97f6dca1328d8b661d055/bacaa22dd274

Evo tu su svi kvizovi

Cvija https://docs.google.com/document/d/1pCK4LPwiY9AZON6lZWK7vFXNB6UogtXnDSOYEmg1w0U/edit?usp=sharing prepisani tocni odgovori, bar koji su oznaceni tocno tam il se sjecam da je bio issue s pitanjem, al ne sjecam se bas svih koji su bili sporni

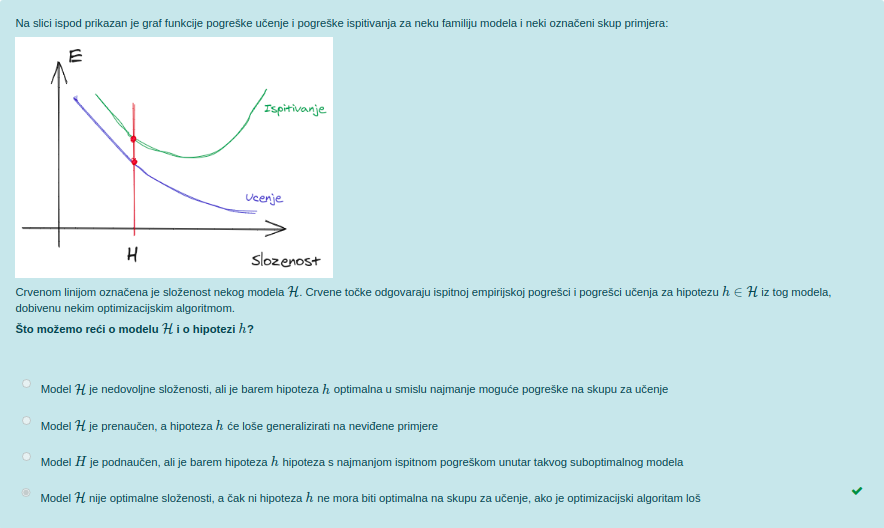
Može mi netko pojasniti ovaj zadatak? Zašto alfa2 nije overfitan?

Bananaking
Moguće je da se u danoj situaciji nalazimo sa lijeve strane od optimalnog modela, oba su podnaučena. Jedino što znamo iz ovoga je da je razlika između greške u učenju i ispitivanju veća kod hiperparametra \alpha_2 nego kod \alpha_1

Ako netko ima vremena objasniti ova 4 zadatka. Meni uopce nije jasno zasšto su ovo točni odgovori.

Hus

Prvi zadatak:
Ako si skiciras problem, vidit ces da je najbolji pravac koji dijeli ove dvije tocke zapravo pravac y=x odnosno u implicitnom obliku -ax+ay=0 gdje je a neka konstanta, jer je implicitni oblik pravca invarijantnan na mnozenje skalarom (ekvivalent toga su homogene koordinate iz IRG-a ako se sjecas; ako ne jebiga).
Druga informacija koju bi trebao znati je naci udaljenost od pravca do tocke: jedna lijepa slatka formula d=h(x) / |w|, gdje je h(x) izlaz hipoteze, a |w| norma vektora tezina. Udaljenost tocke od pravca znamo (ja znam da je sqrt(2) / 2 a od tebe zahtjevam da ako ne znas napamet da izvedes iz geometrije) i lijepo u jednadzbu gore uvrstis neku tocku, recimo (0, 1): sqrt(2) / 2 = (-a*0+a*1) / (sqrt((-a)**2 + (a**2)) i malo se poigras algebarski da dobis a. To ce ti bit jednako w2.
Naravno ista stvar bi trebala doc kao rezultat i ako stavis drugu tocku, to je zato jer (a) matematika tako funkcionira (b) maksimizacija udaljenosti hiperravnine eksplicitno enkodira u nas problem da ce granica prepolavljat udaljenost te dve tocke, odnosno s lijeve i desne strane pravca ce bit ista udaljenost.

Drugi zadatak:
Nadam se da si rjesavao drugi labos koji se ticao logisticke regresije, gdje si uzeo wTx i omotao to oko sigmoide. E sad, sigmoida je poprilicno nelinearna, ali granica koju si (trebao) dobiti je linearna. Zasto je tome tako? Zato jer su ti podaci unutar sigmoide linearni. Dakle, ako ti je funkcija PHI linearna, dobit ces linearnu granicu. Ako je nelinerna, i granica ce bit (perhaps surprisingly) nelinearna. Also, ako ti je PHI nelinearna, a aktivacija f linearna, ponovo granica nije linearna. Podaci su kljuc!

Treci:
Vrlo mehanicki i brainless zadatak. Pomnozis W sa x i dobijes Wx ciji izlaz nazivamo “logiti” (nebitno). Od tih logita racuna se softmax tako da izracunas exp() za svaki element vektora, i onda skupa podijelis sa sumom. Softmax bi ti trebo ispast, ako nisam nesto sjebo, (0.999, 1.026e-10, 1.67e-5). I sad treba samo uzet nas softmax vektor i vektor koji trebamo dobit i s njim u multiclass logistic loss ciju formulu imas u skriptama, labosima ili internetu. Jedino je eto problem sto ja dobijem broj 23 kao rjesenje koji nije ponuden tako da ne znam kj se desilo no postupak je okej haha

Cetvrti zadatak:
adaptivne bazne funkcije == neuronska mreza s jednim skrivenim slojem. ulazni parametri imaju 10 varijabli, svaka adaptivna bazna funkcij ima dakle 10 tezina + 1 bias. Takvih adaptvnih baznih funkcija ima 4, dakle sve skupa 4(10+1) = 44. Zavrsili smo prvi sloj, ai time smo samo iz podataka izvadili znacajke, sto znaci da tek sad idemo u softmax. Znaci sad se pravimo da su ovih 4 “pravi podaci”, dakle trebat ce nam jos 4 tezine i 1 bias. Sve skupa 44+5=49. Puno je lakse ako gledas slikicu i pratis sta se dogada nego ovak napamet rjesavat

Hus
4) Ovo prakticki opisuje neuronsku mrezu sa ulaznom dimenzijom 10, skrivenim slojem dimenzije 3 i izlaznim slojem dimenzije 4. Svaki od slojeva ima svoje biase, pa racunica ispada: (10+1)*3 + (3+1)*4 = 49

Osim toga, ovaj zadatak koji je 3. kod husa, tocan odgovor je 23 i u medjuvremenu su promijenili odgovore tako da je sada i 23 ponudjeno.

InCogNiTo124 kako onda na slici za softmax piše da je w indeksiran s j,k šta ne bi onda trebao w biti drugačiji za različite klase, i zašto ako j ide od 0 mi svejedno na to dodamo bias, jel nije bias uključen kao w0 kad je j=0

InCogNiTo124 Vrlo mehanicki i brainless zadatak. Pomnozis W sa x i dobijes Wx ciji izlaz nazivamo “logiti” (nebitno). Od tih logita racuna se softmax tako da izracunas exp() za svaki element vektora, i onda skupa podijelis sa sumom. Softmax bi ti trebo ispast, ako nisam nesto sjebo, (0.999, 1.026e-10, 1.67e-5). I sad treba samo uzet nas softmax vektor i vektor koji trebamo dobit i s njim u multiclass logistic loss ciju formulu imas u skriptama, labosima ili internetu. Jedino je eto problem sto ja dobijem broj 23 kao rjesenje koji nije ponuden tako da ne znam kj se desilo no postupak je okej haha

meni isto ovo nije jasno, i ja dobijem ~23 generickim softmax postupkom

jel itko to skuzio? jel mozda, slucajno, snajder sjebo?

InCogNiTo124 To je to! Hvala! (meni je isto ispadao u trećem 23 pa sam mislio da sam nesto tesko profulao oko gubitka i modela multinomijalne regresije, no izgleda da nisam jedini pa barem nešto)

InCogNiTo124 Drugi zadatak:
Nadam se da si rjesavao drugi labos koji se ticao logisticke regresije, gdje si uzeo wTx i omotao to oko sigmoide. E sad, sigmoida je poprilicno nelinearna, ali granica koju si (trebao) dobiti je linearna. Zasto je tome tako? Zato jer su ti podaci unutar sigmoide linearni. Dakle, ako ti je funkcija PHI linearna, dobit ces linearnu granicu. Ako je nelinerna, i granica ce bit (perhaps surprisingly) nelinearna. Also, ako ti je PHI nelinearna, a PHI linearna, ponovo granice nije linearna. Podaci su kljuc!

Pročitala sam ovo nekoliko puta i razmislila o tome, ali zaista mi ne sjeda.
Nije mi jasno, ako imamo sigmoidu ili ako je npr. f neka jako divlja nelinearna funkcija (šta ja znam, sinusi, kosinus, apsolutne vrijednosti, šta se već sve da skombinirati u jednu funkciju), kako unatoč tome funkcija uspije dati neku linearnu granicu samo zbog toga što su podaci linearni?

InCogNiTo124 Treci zadatak, 23 je rješenje promijenili su zadatak

InCogNiTo124 Dakle, ako ti je funkcija PHI linearna, dobit ces linearnu granicu. Ako je nelinerna, i granica ce bit (perhaps surprisingly) nelinearna. Also, ako ti je PHI nelinearna, a PHI linearna, ponovo granice nije linearna.

Mislim da si neku riječ falio, možeš srediti to? 🙂

sphera prvo pitanje, svaki stupac u matrici W ti je jedan model za jednu klasu. Onda se oni svi skupe i pretvore softmaxom u distribuciju po klasama

Drugo pitanje, to su sad vec detalji koji nisu nikad nigdje konzistentni, konkretno u ovom slucaju cini mi se da nema biasa pa da je prvi element od 0 indeksiran

Amajli 1.55 je najblizi 23 tak da je zato xD

Amajli sad sam drugi put pokrenula kviz i druga su rjesenja pod tim zadatkom, netko prijavio il oni skuzili I guess