Studoši

a_ko_si_ti kak dobijem ovaj |w|, jer u najboljem slucaju mi ispadne 0.56 a treba ispast po ovome 0.51

Ζ ε ύ ς Pošto se radi o L1 regularizaciji, |w| je apsolutna suma svih elemenata od w (osim w0 jer njega ne skaliramo). To ti daje 0.94+0.08=1.02, i onda iz formule o gubitku vidis da se ubaci |w|/2=0.56.

Jel moze pomoc oko ovog iz MI-ja (8.)

Jel itko moze objasniti 10., 17. i 24. iz ovogodišnjeg MI-a kako se rade.
10.

Tocno je 50/32 i 25/16. Ja stalno dobivam 50/21. Za OVR uzmem N klasifikatora (4) i svaki se trenira sa 1000 primjera, sto daje za svaki Grammovu matricu od 1 000 000 elemenata, i tako puta 4 puta (4 000 000). Za OVR imam K povrh 2 (6) klasifikatora, i imaju razlicito elemenata, ovisno o broju primjera(400+400, 400+100 * 4, i 100+100). U sumi dobijem 1 680 000 elemenata u Grammovoj matrici i iz toga omjer 50:21

17.

Točan je A. Ovdje sam izračunao h(x) za svaki x, po tome odredio koji je y, i onda to ubacio u formulu za ovisnost w i alpha 5. stranica ovdje. Time sam dobio sistem od 4 jednadžbe sa 4 nepoznanice (alphe) i od toga uvijek dobio da nema rješenja. Jel to točan način za radit pa ja krivo rješavam sistem jednadžbi ili ima neki drugi način?

24.

Ovdje je točno pod D. Mogu navuć brojke al mi nije baš 100% jasno. 501 parametar optimazacije mi je jasno jer imamo 500 jezgrenih funkcija (za svaki primjer jednu) u jezgrenom stroju, plus φ1=1. Al kako su došli do 3079 parametara? Sta ne bi bilo da za svaki od 38 prototipa imamo samo po jedan skalar w?

Moze pomoc oko (15.) u MI-ju?

racunao sam ali dobijem da moram skalar pomozit dalje s vektorom fi(x) a ne znam dal radim nesto krivo ili?

Ζ ε ύ ς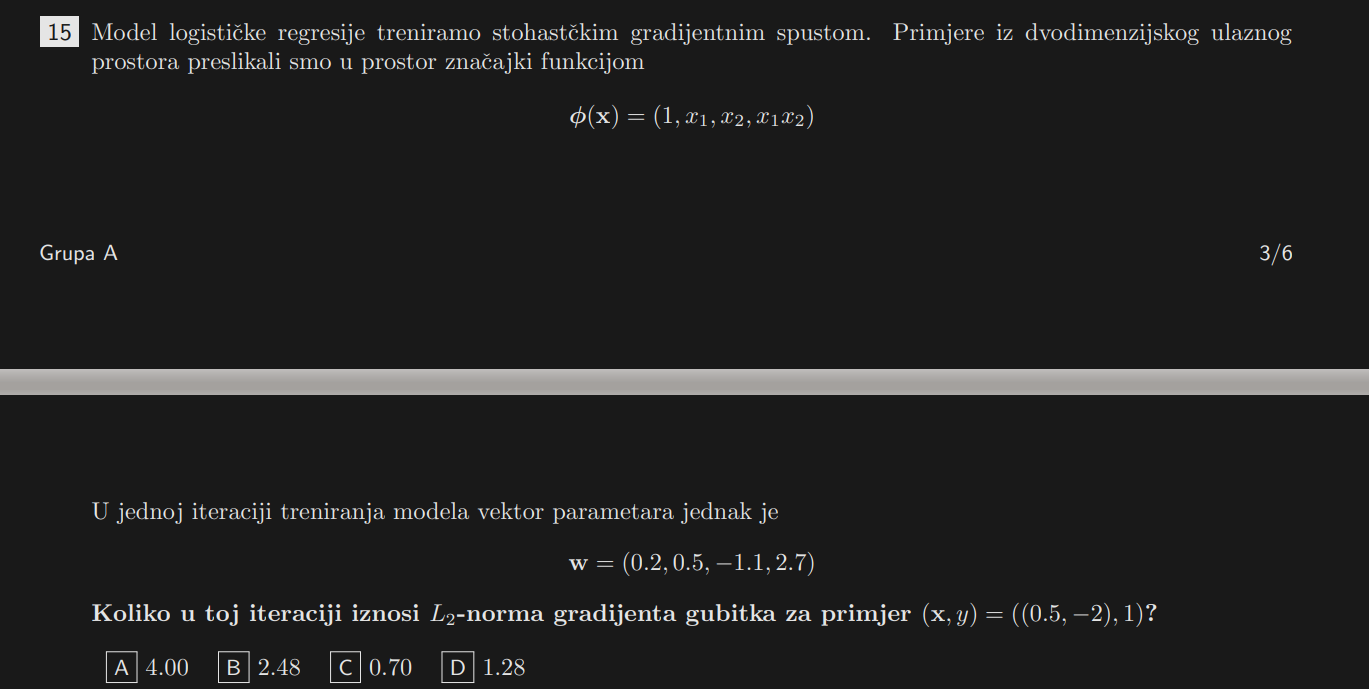
1.28 je rj.

Moze pomoc oko (16.) iz MI-ja

dobio sam da je w2 = 5 a u rj. je -5

Ζ ε ύ ς Ja sam to grafički rješio. Jednom kad nacrtas tocke, lako se vidi koja je hiperravnina, a onda i njena normala (w).
Al analitički gledano: Odkud ti da je skalarni umnožak 0? Ta dva vektora nisu okomita, nego paralelna.

a_ko_si_ti ima u formulama negdje navedeno al moguce da sam ja sjebo

a_ko_si_ti daj kad se vec samo ti i ja dopamo ovdje jel mo mozes pomoc oko ostalih zadataka ili ako imas postupak MI-ja da sherash tu ili nekaj

a_ko_si_ti btw rijesio sam, krivo sam napisao krate se w0 i w0 i dobijes iz toga jednadzbu da je -w2 = w1

Zna li netko objasniti kod linearne regresije zašto je sustav nekonzistentan ako vrijedi rang(X) < rang(X|y), gdje je X matrica dizajna, a y vektor oznaka?

TentationeM jedan od super primjera di znanje linearne dobro dode

promatramo sljedeci slucaj: broj redaka je veci od broja stupaca (dakle imamo vise primjera nego znacajki). rang matrice je min(broj redaka, broj stupaca), dakle u ovom slucaju rang == broj stupaca. dodavanjem jednog stupca povecali smo rang za jedan.
gdje tu u cijelu pricu ulazi konzistentnost? ako imamo vise redaka od stupaca, u jeziku linearne algebre to znaci kao da imas vise jednadzbi od nepoznanica (dakle mozes imat x1 .. x5, ali 20 jednadzbi) za takav sustav jednadzbi kazemo da je preodreden odnosno inkonzistentan.
jos jednom ukratko, ako se rang matrice poveca kad dodas stupac, znaci da ima manje stupaca od redaka, sto znaci da imas vise jednadzbi od varijabli, sto znaci da ti je sustav inkonzistentan

skroz druga prica se dogada u drugom slucaju, ako je broj redaka manji od broja stupaca (imas manje primjera nego znacajki). Tada je rang matrice == broju primjera (a ne znacajki, kao gore). stoga, dodavanjem novog stupca ne mjenja se rang. u tom slucaju (ako na takvu matricu gledas kao sustav jednadzbi) sustav vise nije inkonzistentan, vec je pododređen (razmisli - ako imas 3 jednadzbe s 4 nepoznanice, ne mozes ih rjesit sve 4 nikako; zato pododreden. za takav sustav mozes nac x4 za svaki od x1..x3 koji zadovoljava sustav jednadzbi)

procitaj polako i po potrebi nacrtaj si o cem pricam, jednom kad skuzis ima savrseno smisla, makar zvuci komplicirano

Nisu stavili ispit za zira u repo. Ja sam uspio par racunskih zadatka pretezito iz 1. ciklusa prepisat s ponudenim odg. Mogli bi napravit neki kolektivni dokument ili tu skupa probat rijesit te zadatke i mi i zi pa da ostane narastajima poslje nas. #djecaSUBuducnost, slikam ove zadatke pa ih naknadno tu objavim

Ζ ε ύ ς https://www.fer.unizg.hr/_download/repository/SU-2020-1IR.pdf
Tu je ispit

U ulaznom prostoru X = {0, 1}³ definiramo klasif model: h(x; w) = 1(w0 + w1x1 + w2x2 + w3*x3 >= 0)
Koja je dimenzija prostora parametara te koliko razlicitih hipoteza postoji u ovom modelu?
Odg: Dim prostora parametara je 4 (jer ih je 4), hipoteza ima manje od 256. Kako dobijem broj hipoteza? Na primjeru je riješen onaj primjer sa 2 dimenzijskim ulaznim prostorom pa je donekle jasno zašto ih je 14 a ne 16 (2 xora ne mogu pravcem klasificirati), ali kako je to matematički za više dimenzionalan ulazni prostor?

Bananaking

Peta bilješka na kraju skripte Osnovni koncepti:
"Razlicite hipoteze imat ce razlicite vektore parametara θ. Medutim, razliciti vektori parametara θ ne
moraju nuzno davati razlicite hipoteze. Na primjer, ako je ulazni prostor diskretan (npr. X = N
n), onda mozemo imati pravce koji su malo razliciti (dakle parametri θ im se razlikuju), ali ipak daju
identicnu klasifikaciju primjera u dvije klase, tj. funkcija h je identicna (kako je uobicajeno, jednakost
funkcije ovdje definiramo ekstenzionalno: dvije funkcije su jednake ako jednako preslikavaju elemente
iz domene u kodomenu. To znaci da razliciti θ mogu dati identicne funkcije"

Dimenzija prostora parameta je 4, ulazni prostor je diskretan (ima 8 različitih ulaza) i bitno je samo jel h(x) veći ili manji od 0(sve hipoteze koje za tih 8 ulaznih primjera daju iste klasifikacije su zapravo jedna hipoteza)
U principu je pitanje na koliko načina možeš klasificirati tih 8 ulaza u dvije klase i to možeš napraviti na 2⁸ načina (256)
od klasifikacije 0,0,0,0,0,0,0,0 do klasifikacije 1,1,1,1,1,1,1,1 i sve između.
Ja sam si ovako protumačio zadatak, ne znam jel točno moje razmisljanje.

SimpleRick

Bananaking
Pitao sam ovdje sličan primjer ali moram priznati da mi nije jasno kako rješavati općeniti slučaj ovakvog zadatka. Evo primjer iz ovogodišnjeg međuispita. Pokušao sam razmišljati “na koliko načina možemo klasificirati ulazne primjere”, kako je X = {0,1}³ njih ima 2³ = 8, mislio sam možda za prvu zagradu x1 može biti manji od fi 1,1, između ili veći, isto za drugu i treću zagradu pa nešto tipa 3C1 + 3C1 + 3C1 = 9 + ?

Ellie Može netko ovo primjeniti na zadatak s roka?
Po meni bi išlo 1 (dummy) + 6 (linearnih) + 6 (kvadratnih) + 6C2 (parovi) * 2² (kombinacije kvadrata nad njima npr x1×2, x1² ×2, x1×2², x1² ×2²) + 6C3 (trojke) * 2³ (kombinacije kvadrata) = 233 = očito krivo, treba biti A) 79.
Pretpostavljam da od 7 značajki jednu trebamo izbaciti jer su iz x5 ×6 i x7 možemo jednu dobiti pomoću druge dvije. Također pretpostavka da štednja u kunama i devizna štednja u eurima nije isto ofc nego 2 računa.

Bananaking Sorry, ne sjecam se vise kako su se rjesavali takvi zadatci. Your guess is as good as mine :/

Bananaking kombinacije parova i trojki gledas ovako n!/((n-2)!x2! I za trojke n!/((n-3)!x3!

Bananaking pokusavao sam ga rijesit ali uvijek dobijem tipa 71 ili tako nesto blizu… ugl kak sam radio makno sam 2 znacajke za stednju i za preostala dugovanja. Dobio sam 5 + 5 + 1 ona klasika i 60 u kombinacijama ovakvim… sad ako ti to ista pomaze da skuzis nkj jebeno bi bilo da mi objasnis haha

Zadnji pokušaj prije nego prestanem postati jer nitko ovo ne uči za jesen ili ne prati temu: zna netko objasniti ovaj zadatak? Odgovor je pod D), pretpostavljam da ide funkcija preslikavanja 1 jer ima kvadratne članove a podaci iz D nisu linearno odvojivi. Ali zašto Perceptron? Zato što perceptron “kažnjava samo netočno klasificirane primjere (za razliku od regresije)” ?

Također: ako netko ima riješene moodle zadatke ili koji ispit bilo bi super to uploadati, bar dok su ispiti ovako više računski na zaokruživanje možda se i da nešto naučiti po primjerima a ne doktoriranjem teorije prije prelaska na zadatke.

Bananaking
Odgovor bi trebao biti D (perceptron i preslikavanje PHI 1 ).
Moje objašnjenje je da perceptron i logistička regresija moraju imati linearno odvojive podatke kako bi učenje konvergiralo (kada podaci nisu linearno odvojivi radi se preslikavanje u prostor di su linearno odvojivi) .
prvo preslikavanje ne radi ništa, samo dodaje dummy značajku i to je obična matrica dizajna.
Treče preslikavanje je u prostor s 3 dimenzije (interakcijska značajka je x1×2 je uvijek nula zato što je ili x1 ili x2 u svakom primjeru nula). podaci su i dalje linearno neodvojivi.
Drugo preslikavanje rješava problem linearnosti ( pretpostavljam zbog kvadratnih baznih funckija ) i onda učenje perceptrona može konvergirati.

SimpleRick

Bananaking

ja radim za jesen, ako ste za imam neki online dokument pa mozemo tamo komentirat i radit

SimpleRick Ok ali zašto ne bi bilo LR i phi1 preslikavanje?

Bananaking
Nisam dobro pogledao odgovore, ne znam zašto nije LR