Studoši

Moze objasnjenje?

Rene Granica između klasa je krivulja definirana jednadžbom h(x)=0. Ta krivulja je pravac ako je funkcija \phi linearna

zasto ovdje B ne bi bilo točno?

[obrisani korisnik] Za različite parametre možes dobiti i istu funkciju h

a ovo ako netko zna logiku? prvo sam mislio da B uvodi nelinearnost pa zato, ali nije istina jer se koristi ova True/False fja

nvm skuzio valjda, to je zato sto se u B moze dogodit da se pomnože lossevi s ispravnima i onda rezultat bude 0 sve skupa

[obrisani korisnik] Pitanje se svodi na to koliko najviše predikcija možeš natjerati da istovremeno budu 0 na zadanom skupu. Drugi model je zapravo skup AND-ova hipoteza iz prvog modela, pa je logično da može imati više nula (skup nula je unija)

BillIK Kako računaš w0?

[obrisani korisnik] pročitaj dretvu viliml

kako je ovdje VS veci od 1? nije li nacrtano zelenim jedina ravnina koja ce tocno odvojiti sve mogucnosti uz pretpostavku linearne odvojivosti

[obrisani korisnik]

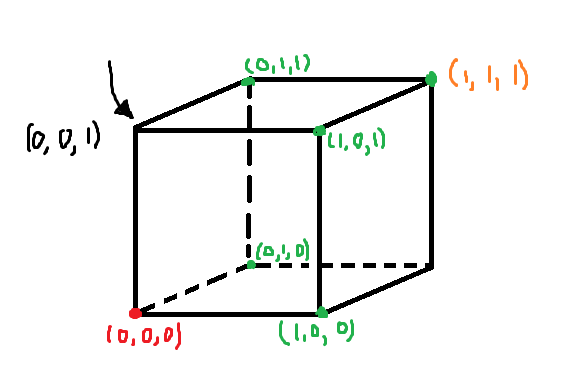
Mislim da si samo pogrijesio u oznacavanju tocaka jer ja sam dobio ovakvu skicu u kojoj onda imas dvije hipoteze u version spaceu.

DZ1: Model takoder nazivamo prostorom inacica, a dimenzija tog prostora jednaka je cemu?

Arya broju parametara.

jel ne bi ovdje trebalo biti L(0, 1) > L(1, 0)? nije li redak == stvarni primjeri, a stupac predikcije

[obrisani korisnik] Nebi trebalo biti L(0, 1)> L(1, 0) . U ovom zadatku treba skuzit da ti je bitnije imat sto manje false negativa jer ne zelis da tvoj klasifikator nekome ne otkrije karcinom, a zapravo ga ima. S druge strane nije ti toliko bitno ako nekom dijagnosticiras karcinom ako ga nema jer ce vjerojatno ic na neke dodatne pretrage da potvrdi to. Zbog toga zelis vise kaznjavati klasifikator ako napravi ovu prvu pogresku, a drugu manje i to upravo odgovara odnosima gubitka L(1, 0) > L(0, 1) .

Jel netko shvatio šta znači izraz “do na …” jer sam vidio na hrpu mjesta da to spominju, ali uopće ne mogu skužit šta predstavlja

Jaster111

Mislim da to možeš čitat kao izuzev, osim.

Jaster111 “isto do na X” općenito znači da mijenjanjem X-a prelaziš iz jednog u drugo. Ovdje je jedan izraz jednak drugom pomnoženom s C.

[obrisani korisnik] Dragi prijatelj strojnog učenja Kad se linearna regresija koristi za klasifikaciju, odmah već mora imati aktivacijsku funkciju. U skripti se koristi funkcija \mathbf{1}\{\alpha\ge0.5\}, ali to je ekvivalentno step funkciji do na promjenu w0 i preimenovanje izlaznih klasa iz 0/1 u =+-1 (Jaster111 ) znači algoritam ekvivalentan perceptronu se može dobiti bez promjene aktivacijske funkcije.

sheriffHorsey to me i muči, svjestan sam ja da je veći problem false negative, ali po ovoj matrici ne vidim kak je to ispravno rjesenje:

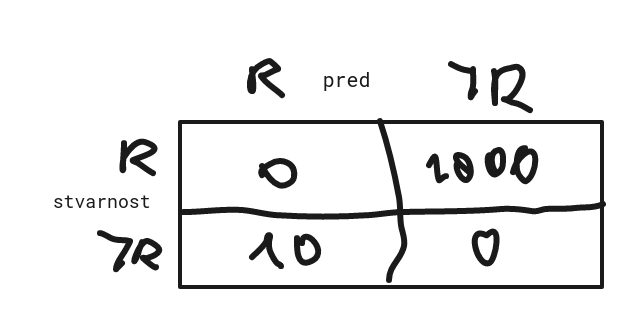
osim ako je svejedno kako oznacavamo retke/stupce pa zato ovo moje nije ni ponuđeno?

[obrisani korisnik] Ako ti redak oznacava stvarnu situaciju onda redak 1 znaci da osoba ima karcinom, a recimo da klasifikator to ne skuzi pa je stupac 0, znaci da je to L(1, 0), tj. prvo indeksiras redak pa stupac.

sheriffHorsey aha, zanemario sam da su 0 i 1 oznake klase, ja sam to gledao samo kao indekse u tablici 😃 ty

tomekbeli420
Je li možeš molim te reći kaj točno uvrstiš ovdje jer nemrem skužit nikak
(prebacivanje iz dualnog u primarni oblik)

Znači npr. kak si došo do w1? Što si točno uvrstio, koje brojeve?

Ivančica
w_1 = \sum_{i=1}^{N} \alpha_i y^{(i)} x^{(i)}_1

Ivančica e sry tek sad vidio

vektorsko zbrajanje, dakle \alpha_i i y^{(i)} su skalari, a \mathbf{x}^{(i)} su vektori
\mathbf{w} = \alpha_1 y^{(1)} \mathbf{x}^{(1)} + \alpha_2 y^{(2)} \mathbf{x}^{(2)} + \alpha_3 y^{(3)} \mathbf{x}^{(3)} \\ \mathbf{w} = 0 \cdot (-1) (-1, 3, 6) + 0.01 \cdot (-1) (-4, 4, 4) + 0.01 \cdot 1 (-2, 4, 1) \\ \mathbf{w} = (0, 0, 0) + (0.04, -0.04, -0.04) + (-0.02, 0.04, 0.01) = (0.02, 0, -0.03)

I onda kako je \mathbf{w} = \left(w_1, w_2, w_3\right) odavdje iščitaš sve šta te zanima

Zna netko ova dva?

Rene Imaš ovaj prvi detaljno objašnjen u snimci sa zadnje rekapitulacije na teamsima, uglavnom za ovu jezgru se izvede preslikavanje (x1², sqrt(2)x1x2, x2²), a sa polinomom dobiješ standardno (1, x1, x2, x1², x1×2, x2²) i onda ovom prvom dodaš samo 3 nule na početak jer tih članova tamo nemaš i onda ti je euklidska udaljenost zbroj kvadrata razlike za svaki od njih. Kad uvrstiš primjer dobiješ za jezgreni (0,0,0,0,1,0), a za ovaj (1,1,0,0,1,0) i onda je to korijen iz 1² + 1² i to ti je rješenje.

Rene Za drugi zadatak, uvijek je moguće barem teoretski izračunati udaljenost
d(\mathbf{x})=\frac{h(\mathbf{x})}{||\mathbf{w}||}=\frac{\sum_i{\alpha_i y^{(i)} \kappa(\mathbf{x},\mathbf{x}^{(i)} )}+w_0}{\sqrt{\sum_i{\sum_j{\alpha_i \alpha_j y^{(i)} y^{(j)} \kappa(\mathbf{x}^{(i)}, \mathbf{x}^{(j)} )}}}}
Možda se referenciraju na to da je prostor značajki za Gaussovu jezgru neprebrojivo-beskonačno-dimenzionalan pa sumiranje po dimenzijama i slične stvari nisu zapravo definirane, ali s konkretnom hipotezom će se sve događati u konačno- ili prebrojivo-beskonačno-dimenzionalnom podprostoru gdje sve sume koje nam trebaju konvergiraju…