Studoši

Može netko raspisati ovaj, čini se jednostavno ali ne znam kako tretirati ovu prvu i zadnju uvjetnu nezavisnost

Bananaking

sori ako nije čitljivo

jel uspio netko? nema šanse da ikako pogodim tih 64

tomekbeli420
znaci za \mathcal{H}_0 imas dio koji se odnosi na numericke znacajke: \frac{2 \cdot 3}{2} + 2\cdot 2 + 2 - 1 = 8
u tom izrazu redom imas parametre za dijeljenu kovarijacijsku matricu (cuvas dijagonalu i jedan trokut), za svaku klasu po jedan vektor sredine \mathbf{\mu}_k i jos K - 1 parametar za apriorne vjerojatnosti
nakon ovoga ide dio za kategoricke znacajke: (3\cdot 2\cdot 2 - 1) \cdot 2 = 22
ovdje moras isprobat sve kombinacije vrijednosti svih znacajki osim jedne koju mozes dobit iz uvjeta da se vjerojatnosti zbrajaju u 1 i to jos pomnozit s brojem klasa

sljedeci je model \mathcal{H}_1:
kod numerickih znacajki se sad mijenja prica jer je sad kovarijacijska matrica dijeljena ali i dijagonalna pa ti vise ne treba trokut, ali ostalo ostaje isto: 2 + 2 \cdot 2 + 2 -1 = 7
kod kategorickih znacajki su sad x_1 i x_4 združene pa se smanjuje broj kombinacija: [(3\cdot 2 - 1) + (2-1)]\cdot 2 = 12

i na kraju \mathcal{H}_2:
opet vrijedi isto za numericke kao i u prethodnom modelu: 2 + 2 \cdot 2 + 2 -1 = 7
kod kategorickih se pak jos vise smanjuje broj parametara: [(3-1) + (2-1) + (2-1) ] \cdot 2 = 8

Na kraju kad se sve sumira: (8+22) + (7+12) + (7+8) = 64 parametra

Geralt of Rivia Dakle kod naivnog Bayesovog klasifikatora vrijedi

P \left(\mathbf{x}, y\right) = P \left(x_1, x_2, x_3, x_4, y\right) = P (y) P (x_1 \mid y) P (x_2 \mid y) P (x_3 \mid y) P (x_4 \mid y)

E a sad ove vjerojatnosti P (x_k \mid y) su vjerojatnosti kategoričke (ili Bernoullijeve ako su moguće samo 2 vrijednosti) slučajne varijable X_k, koje se procjenjuju Laplaceovim zaglađivanjem (MAP procjena sa onim alfama 2).
U nazivnik ide
ukupan broj primjera sa oznakom y (kako nas zanima y=1 gledaš ukupan broj primjera koji imaju tu oznaku, dakle ima ih 3)
plus
ukupan broj različitih vrijednosti varijable x_k. Ova dva koja si zaokružio su faktori koji predstavljaju P(x_1 = \text{"Istra"} \mid y=1) i P(x_2 = \text{"ne"} \mid y=1)
Dakle za ovaj prvi faktor x_1 ima moguće 3 vrijednosti (Kvarner Dalmacija Istra) zato još stoji +3 a za ovaj drugi faktor x_2 ima moguće 2 vrijednosti (da ne).

sheriffHorsey
Um…. Jasno mi je da je to točno rješenje ali
Neka mi netko objasni kako, na koji način, ovaj komad o \mathcal{H}_0 ne uvodi pretpostavku o uvjetnoj nezavisnosti????????????????????
Ovim postupkom koji si ti naveo bi se združena vjerojatnost faktorizirala kao
P \left(x_1, x_2, x_3, x_4, x_5, y\right) = P (y) P (x_2 ,x_3 \mid y) P (x_1, x_4, x_5 \mid y)
Dakle ove brojke koje si naveo, 1, 8, 22, su upravo brojevi parametara za procjenu ovih faktora
Što nije potpuna faktorizacija bez nekih uvjetnih nezavisnosti. Konkretno ovdje bi onda, čisto gledajući samo ovu faktorizaciju vrijedilo \{x_2, x_3\} \perp \{x_1, x_4, x_5\} \mid y
I kako je sad to točan odgovor ako kaže da \mathcal{H}_0 ne uvodi nikakve pretpostavke o uvjetnoj nezavisnosti???? Ono što sam ja dobio isprve pa sam bio u čudu je broj parametara samo za \mathcal{H}_0 je prelazio sve ove odgovore.

prx_xD jos skrolanja 5 sekundi gore i nasao bi 4. sheriffHorsey

Je li ima netko raspisano rjesenje ovog zadatka (zavrsni prosle godine) sa uzajamnom informacijom? U predavanju asistent samo preleti preko njega, a u onom doc fileu su napisana gotova rjesenja. Takoder postupak rjesavanja i brojevi od asistenta sa predavanja se razlikuje od onih iz doc filea za vjerojatnost x2.

cajaznun Znaci polunaivan bayesov klasifikator je slican kao naivan Bayesov klasifikator. Znaci rastavlja P(x_1, x_2, x_3, y) = P(y) P(x_1 \mid y) P(x_2 \mid y) P(x_3 \mid y) ako su sve varijable uvjetno nezavisne. Ako nisu, onda te zdruzi, npr recimo da su x_2 i x_3 uvjetno zavisne onda bi zajednicka vjerojatnost bila: P(x_1, x_2, x_3, y) = P(y) P(x_1 \mid y) P(x_2, x_3 \mid y)
Problem koji se dogadja je da je tesko odrediti koje su varijable uvjetno zavisne i onda postoje razliciti postupci objasnjeni u skripti da sad ne ulazim u detalje. U zadatku kaze da su varijable uvjetno zavisne ako je I(x_i, x_j) > 0.01 tj. uzajamna informacija veca od 0.01. Sad samo treba izracunati I za svaki par i vidjeti koji su parovi zavisni. Njih cemo zdruziti u faktorizaciji P(x_1, x_2, x_3, y) poslije.
I(X, Y) se računa kao \sum{P(X, Y) ln \frac{P(X, Y)}{P(X)P(Y)}} za svaku vrijednost X i Y.
Primjerice:
I(x_1, x_2) = P(x_1=0, x_2=0) ln \frac{P(x_1=0, x_2=0)}{P(x_1=0)P(x_2=0)} +P(x_1=0, x_2=1) ln \frac{P(x_1=0, x_2=1)}{P(x_1=0)P(x_2=1)} +P(x_1=1, x_2=0) ln \frac{P(x_1=1, x_2=0)}{P(x_1=1)P(x_2=0)}+P(x_1=1, x_2=1) ln \frac{P(x_1=1, x_2=1)}{P(x_1=1)P(x_2=1)}
Ne da mi se sad raspisivat dalje detaljno, al iz tablice se mogu odrediti P(x_1, x_2) za svaki par vrijednosti. Npr za (0, 0) samo zbroji kad su x_1, x_2 = 0 za svaki x_3. Slicno i za P(x_1), samo se zbroje sve vrijednosti za svaki x_2 i x_3
Ako je ovo isti zadatak kao u zadacima za vjezbu, dobije se:
I(x_1, x_2)=0.00513164
I(x_1, x_3)=0.03
I(x_2, x_3)=0.00513
iz cega slijeda da su varijable x_1 i x_3 zavisne i faktorizacija je P(x_1, x_2, x_3, y) = P(y) P(x_2 \mid y) P(x_1, x_3 \mid y)

jel bi znao neko ovog objasnit ? nemogu si namapirat ove h1,h2,h3 na one kruznice

𝐓𝐇𝐄 𝐒𝐄𝐂𝐑𝐄𝐓 - 𝐂𝐋𝐔𝐁 ima ga na predavanju ako se ne varam.

Ukratko, u predavanju postoje formule za izračun parametara za razne varijante bayesovog klasifikatora. U te formule uvrštavaš podatke iz zadataka, pa tako usporediš broj parametara.

Što se tiće složenosti, može se zaključiti da je model H2 je jednostavniji od H1 jer je on, prema njegovov definiciji, podskup modela H1. O odnosu H1 i H2 naspram H3 ne možemo baš pametno zaključiti jer oni nisu podskup modela H3.

𝐓𝐇𝐄 𝐒𝐄𝐂𝐑𝐄𝐓 - 𝐂𝐋𝐔𝐁 ne znam o kakvim kruznicama govoris, ali izracunas broj parametara za svaku model:
H1: dijagonalna kovarijacijska za svaku klasu
n * K + nK + K-1 = 109
H2: izotropna ali nije dijeljena
K + nK + K-1 = 69
H3: dijeljena
n(n+1)/2 + n*K + K-1 = 74
Jedini odgovor koji se s ovim poretkom slaze je A

tomekbeli420 Ima smisla ovo sto kazes, ali nije mi uopce jasno kako iskombinirati onda numericke i kategoricke znacajke

sheriffHorsey

tomekbeli420

Imate to rješeno https://docs.google.com/document/d/15drigevvwo3wOvZ3uFZgCAO2hgEHdCUa-a1DTMWV7_k/edit#
Šnajder je i potvrdio da je točno i dobro objašnjeno, makar ja osobno ne razumijem neke dijelove objašnjenja.

Glupo pitanje ali kod algoritma k-sredina, kriterijska funkcija J je L2-norma, ako je centroid (1,2) a primjer x = (1,1), koliko iznosi J za taj primjer?

Bananaking zbroj kvadriranih euklidskih udaljenosti (euklidska udaljenost = L2 norma vektorske razlike), dakle ne korjenuje se zbroj kvadrata po dimenzijama.
\boldsymbol{\mu} = (1, 2) \qquad \mathbf{x} = (1, 1) \\ {\Vert \mathbf{x} - \boldsymbol{\mu} \Vert} ^2 = (1-1)^2 + (2-1)^2 = 1

sopla Super, hvala, ovo p(z|v,w,x,y) me zanimalo, imamo da je P(z|w,x,y) = P(z|x,y) ali nije mi bilo jasno jel možemo i v izbaciti

tomekbeli420 Pokušavam ovaj riješiti, nisam vidio na predavanjima da su riješili baš iteracije k-sredina, ovako sam ga ja shvatio ali očito nisam dobro

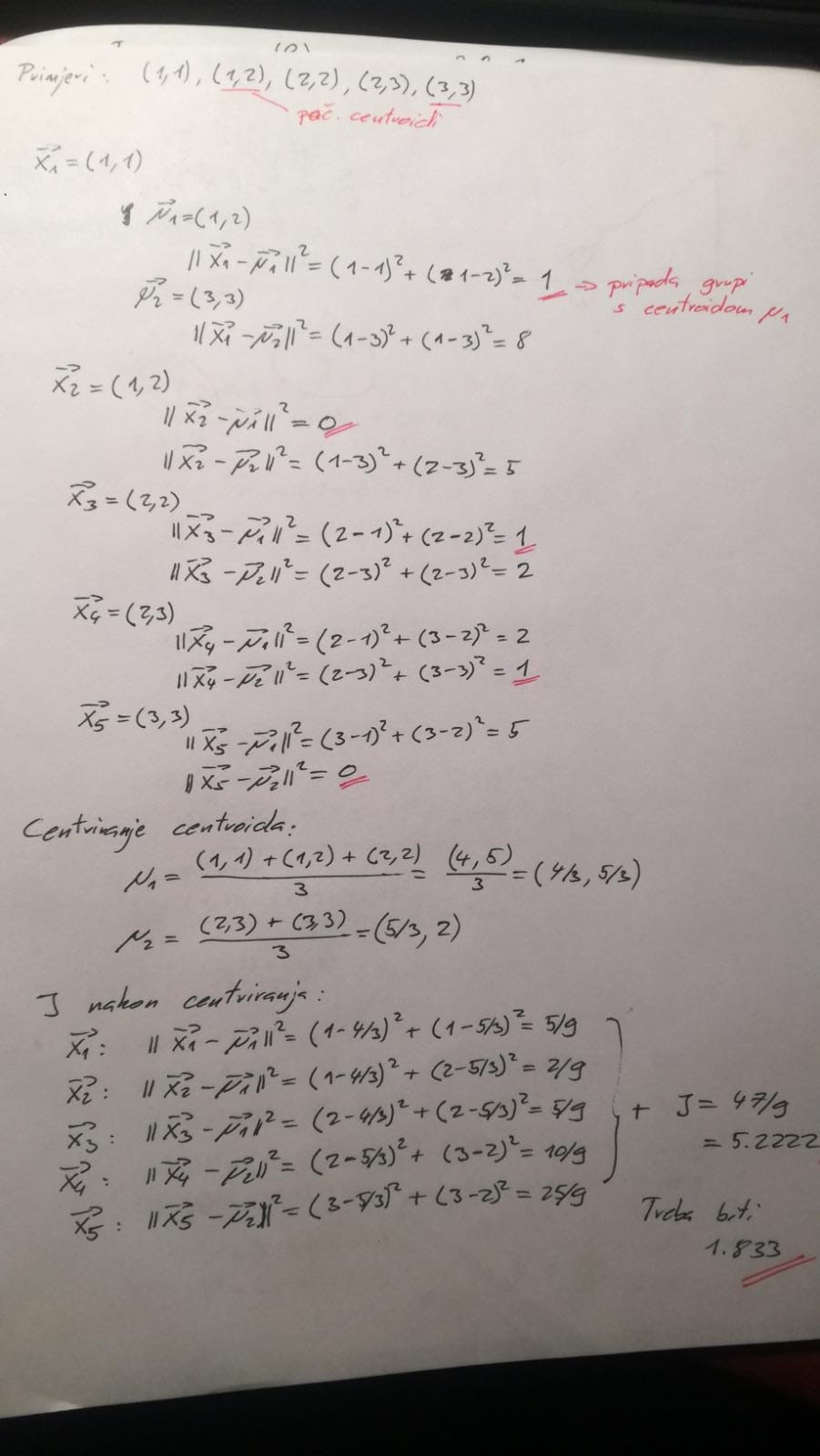
EDIT: ups, u centriranju za mi 2 je u nazivniku 2 a ne 3 hahah, sad sve valja, nek ostane post na moju sramotu ali možda nekom pomogne

sheriffHorsey e dakle ja sam inicijalno ovako to iskombinirao
dakle hoćemo računati neke uvjetne vjerojatnosti i moramo onda parametre procijeniti
e sad je pitanje kako faktorizaciju napraviti, jer nije moguće kao u onom primjeru u skripti napraviti sve moguće kombinacije vektora \mathbf{x} = (x_1, x_2, x_3, x_4, x_5) jer takvih ima neprebrojivo mnogo zbog x_2 i x_3

E sad sam si razmisljao okej kako napraviti (potpunu) faktorizaciju a da opet mogu prikazati sve to u konačnom broju parametara
Pa mislim si okej ne mogu imati situaciju gdje u uvjetnom dijelu imam neku kontinuiranu varijablu, jer onda opet imam beskonačno kombinacija
Dakle onda moram imati faktor P(x_2, x_3 \mid x_1, x_4, x_5, y) i ovo se da u konačno mnogo parametara prikazati. Za svaku kombinaciju ovih uvjetnih varijabli imat ću jedan 2D Gausijan

Onda konačna faktorizacija bi bila
P(x_1, x_2, x_3, x_4, x_5, y) = P(y) P(x_1, x_4, x_5 \mid y) P(x_2, x_3 \mid x_1, x_4, x_5, y)

Za računati prvi faktor treba 1 parametar
Za drugi treba 22, kao što i kod tvog postupka (3*2*2-1 kombinacija za svaku klasu)
E a za ovaj treći, treba nam dakle 3*2*2*2 = 24 dvodimenzionalnih Gausijana za svaku kombinaciju
Dakle 24 dvodimenzionalnih lokacija + jedna dijeljena kovarijacijska matrica od 3 parametra = 24*2+3 = 51 parametar
1+22+51 = 74
I to je samo za \mathcal{H}_0

Evo ovo je moje mišljenje što bi trebalo biti dobro, ovo njihovo fakat nema smisla…

Dootz di točno, ja ne vidim da uopće se pojavljuje taj zadatak u tom docu
edit: nvm našao sam sad gledam

ma kakvi nema šanse da je ovo objašnjenje dobro, čini mi se da je i on uključio uvjetne nezavisnosti, da ima vremena popričao bih s njim, uvjeren sam 100% da je sjebao

tomekbeli420 Stranica 16

moze netko objasnit ova 2 zadatka iz zzv-ova Bayesov Klasifikator 2
imaju rjesenja u docu al mi nisu jasna
sada sam vidio da je Cubi ovjasnio 5 zadatak al moze netko 4