Studoši

koji je neutralni element za xor?

Ollie rekao bih 0, jer

0 xor A -> A

0 xor 1 -> 1
0 xor 0 -> 0

Pepper

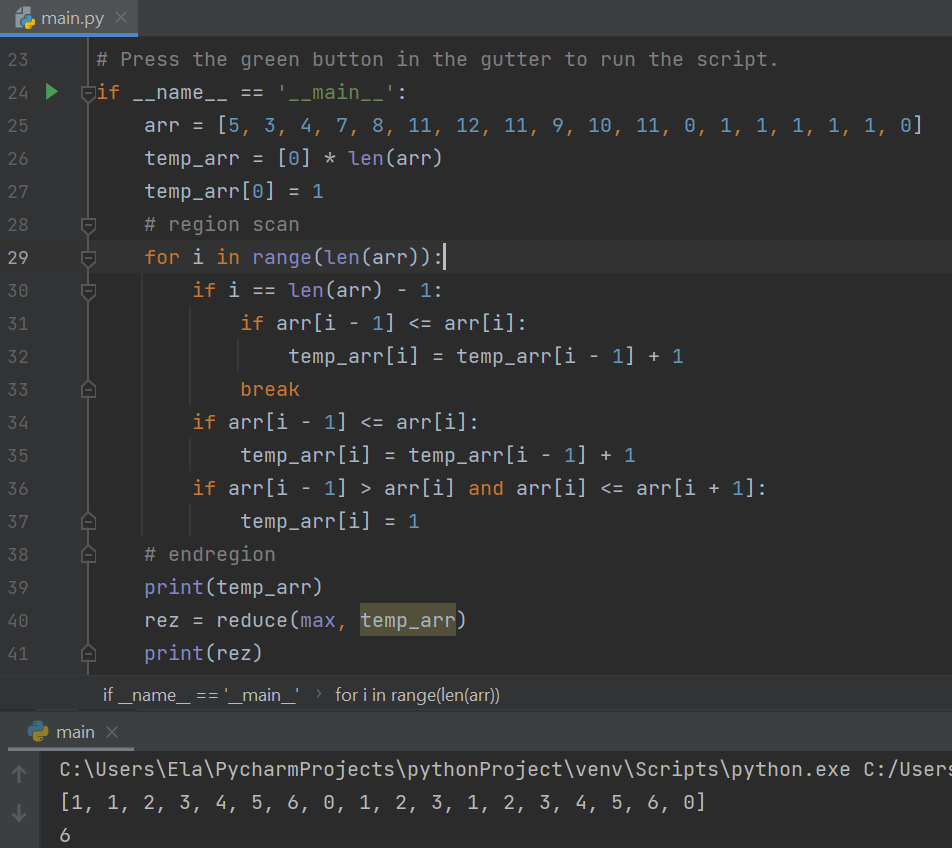
ja bih to ovako

MsBrightside ali to je slijedno i ne može se paralelizirati, za temp_arr[i] ti uvijek treba temp_arr[i-1]

Pepper Pogledaj najnovije rješenje koje sam dodao u google dokument za 1.10. Samo treba zamjeniti niz isti s uzlazni i radit će i na ovom zadatku.
Logika je zapravo fundamentalno više manje ista kao ovo od MsBrightside samo sam tu for petlju izveo u više koraka koji se zapravo mogu paralelizirati.

MsBrightside Aha ček, misliš li tu for petlju realizirati kao scan? Ili što znače ti komentari?
Je li ta operacija uopće asociativna…? Možda je… Ali trebalo bi to razbiti na dijelove.

Sto ako u algoritmu iskoristimo neki reduce, jel se on uviejk izvodi preko binarnog stabla i ima složenost logn pa onda poveca i slozenost cijelog algoritma na logn?

sekiro slozenost za reduce je uvijek logn tako da kad racunas ukupnu slozenost taj dio koda(reduce operacija) doprinosi ukupnoj slozenosti sa O(logn), za ukupnu slozenost moras gledati i slozenost ostatka koda npr. ako imas i dio koda koji je O(n) onda ce ukupna slozenost biti O(n) + O(logn) = O(n + logn) = O(n) (jer n brze raste od logn)

viliml da, mislila sam ga kao scan, samo mi se nije dalo odvojenu funkciju radit, ja bi rekla da donekle je asocijativna ali ne znam vise

Rene jel mozes poslati link?

MOXY https://docs.google.com/document/d/1TP_lsv4lcYj9Ysbq8PiKXcNN33-9iI3UGD7H3LkDbJ0/edit

aha, mislio sam da ce tu biti i rjesenja MI-jeva, jel netko rijesio MI 2015/16?

MOXY koji ti zadaci trebaju

MsBrightside 4. i 6. za provjeru

MOXY Ako sam ja dobro skontala 6 bi trebao bit
(n/p + d - 1) + B + n/p + (n/p + d - 1) + B
znaci citanje, ograda, lokalne instrukcije, pisanje i ograda.

A 4.

n = [0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0]
    r = [-1] * len(n)
# ovaj for je kao paralelno jer svaki procesor pise samo na svoju lokaciju
    for i in range(len(n)):
        if n[i] == 1:
            r[i] = i
    print(r)
    max1 = reduce(max, r)
    print(max1)
    min1 = reduce(min_reduce, r)
    print(min1)
    one_sum = reduce(sum1, n)
    print(one_sum)
    zeros = max1 - min1 - one_sum + 1
    print(zeros)

Jel’ iko vidi grešku u ovom pristupu za 1.10 (nisam baš skužio kako je +_scan u ostalim rješenjima točan):

PARALELNO(i=0 DO n-1) { 
    isti[i] = 0
    poc[i] = 0
    kraj[i] = 0
    k[i] = P[i] //kopija ulaznog niza
}
PARALELNO(i=0 DO n-2) {
    AKO (P[i] == K[i+1]) {
        isti[i] = 1
    }
}
PARALELNO(i = 0 DO n-1) {
    AKO (i == 0 || isti[i-1] == 0) {
        poc[i] = i // ako je prvi element niza, ili prethodni nije isti kao on, onda je pocetak
    }
    AKO(isti[i] == 0) {
        kraj[i] = i // ako nije isti kao sljedeci, na njegovom indeksu zavrsava podniz
    } INAČE {
        kraj[i] = i + 1 // podniz se "nastavlja"
    }
}
start = MAX_SCAN(poc[]) // pronađi zadnji indeks na kojem je neki podniz započeo
end = MAX_SCAN(kraj[]) // pronađi zadnji indeks na kojem je neki podniz završio
PARALELNO(i = 0 DO n-1) {
    REZ[i] = end[i] - start[i] + 1
}
max = MAX_REDUCE(REZ[])

Primjer izvođenja za niz P[] = [1 2 2 4 7 3 3 3]
isti[] = [0 1 0 0 0 1 1 0]
poc[] = [0 1 0 3 4 5 0 0]
kraj[] = [0 2 2 3 4 6 7 7]
start[] = [0 1 1 3 4 5 5 5]
end[] = [0 2 2 3 4 6 7 7]
rez[] = [1 2 2 1 1 2 3 3]
max = 3

Rene Čini mi se da bi moglo biti točno, ali nekako mi se ne sviđa ovo s kraj[i]=i+1.
Što ti smeta s +_scanom?
Ovo je moje rješenje s google docsa:

isti[N-1] = {}

PARALELNO(i=0 DO n-2)
  isti[i] = 0
  
PARALELNO(i=1 DO n-1)
  AKO(P[i-1] == P[i])
    isti[i-1] = 1

duljina = +_scan(isti[])
    
PARALENO(i=0 DO n-2)
  AKO(isti[i] == 1)
    duljina[i] = 0
    
duljina = max_scan(duljina[])

PARALENO(i=1 DO n-2)
  AKO(isti[i] == 0)
    isti[i] = duljina[i-1] - duljina[i]

duljina = +_scan(isti[])
  
najdulji = 1 + max_reduce(duljina[])

Primjer izvođenja:
isti[]= [0 1 0 0 0 1 1 0]
duljina[] = [0 1 1 1 1 2 3 3]
duljina[] = [0 0 1 1 1 0 0 3]
duljina[] = [0 0 1 1 1 1 1 3]
isti[] = [0 1 -1 0 0 1 1 -2]
duljina = [0 1 0 0 0 1 2 0]

MsBrightside zar neće u min uvijek bit -1?

Ovi zadaci za PRAM koji su tipa “Napisati algoritam za CRCW/EREW PRAM računalo”
Je li ovo znaci napisati 2 algoritma tj 1 za svaku vrstu ili napisati samo 1 algoritam na odabir
Takoder ako treba oba - je li dovoljno napraviti EREW pa ce on raditi i na CRCW ili bas treba prilagodeni za CRCW

anon00 Mislim da je dovoljno napisati samo EREW, u slučaju da ne znaš EREW onda možeš probat CRCW da se skupi neki bod.

Me ne jer sam koristila svoju modificiranu min funkciju
def min_reduce(a, b):
if a == -1:
return b
elif b == -1:
return a
else:
return min(a, b)