Studoši

zajebo sam MI, gledam sad predavanja drugog ciklusa zadnjih nekoliko dana i ništ ne kužim, iz čega je najbolje da učim za završni

ne zelim ti ubit nadu, al ako do sada nisi 2.ciklus nista radio i MI zeznuo mozda bolje da se pripremas samo za rok jer je 2. ciklus malo zahtjevniji(moze biti kako kome). Ovako ti mogu dat tip da spremi kpz, mozes pokupit 9 10 boda, pogledaj one skripte iz labosa i proslogodisnje kpz, normalna razdioba ti nije takav problem, prouci to malo sto je u knjizi i pogledaj stare ispite jer ti dolaze zadaci na slicnu foru sto se definitivno moze rjesit. Sto se tice slucajnih vektora prodi knjigu i rjesi dodatne zadatke sto su na ferwebu, mislim da su jako dobri za shvatit i mozda brzo shvatis ako uspijes. 9 cjelina je podosta zahtjevna i puna teorije, mislim da zahtjeva vremena…iz 10 pogledaj prodi primjere kad je statistika nepristrana/valjana, takoder su dobri primjeri u onim dodatnim zadacima…ovo je sto ti mogu rec da napravis u ovih par dana i sto mislim da je najbolje

Jel zna neko kako bi se ovo rješilo?

DazedAndConfused domena slucajnog vektora (X, Y) ti je trokut izmedu pravaca x=0, y=1 i y=x. Dalje ide vise manje po spranci, f(x, y) = f(x)•f(y|x), pa to u integral i tak

InCogNiTo124 I krenuo sam tako, ali kako dobijem f(y|x) ?

DazedAndConfused “y se bira na srecu iz intervala” == svaki put kad to procitas, nesto u tebi mora vristat uniformna razdioba

Funkcija gustoce uniformne razdiobe je 1/(duljina intervala)

dakle, u ovom slucaju, f(y|x) = 1/(1-x)

1) ovaj kpz se pise samo na ZI, ne i na rokovima?
2) kolko vremena treba za naucit ovo za 2 na roku i kojom taktikom je najbolje ic?

mihamih
1) kpz se piše samo na ZI
2) 5-6 dana punog gasa ako si potpuno neupućen u gradivo, najbolja taktika stari ispiti s fer3 programa, fer2 se razlikuje, eventualno nauči neke dokaze koji se često pojavljuju npr. izvod bayesa je bio 2-3 puta prošle godine, 7. i 8. lekcija mislim da su najteže pa eventualno to nemoj učit

Ulazi li u KPZ nepristrana procjena standardnog odstupanja?

Jel neko mozda preuzeo predavanja od 8. nadalje, pa da može podijelit kao što je @anon00 prije međuispita? Izgleda da je sa ms streama nestalo sve osim vježbi i “labosa”.

Dough_Dough klikni na profile profesora. tamo su uploadali

Kakve su ove snimke labosa na teamsu? Ce mi bit dovoljno samo njih pogledati za KPZ ako sam prosao 11. i 12. cjelinu?

zna netko možda kako riješiti ovo? odgovor je n>=45 . pokušao sam uvrstiti u interval povjerenja , ali nešto mi fali.

krampus aritmeticka sredina ima varijancu sigma²/n, mozda to?

krampus nema to veze s intervalima povjerenja, to se rješava ovako:

označimo sa X_i broj na kocki u i-tom bacanju. To je diskretna slučajna varijabla koja ima uniformnu razdiobu i može poprimiti 6 vrijednosti, dakle sve sa jednakom vjerojatnošću:
X_i \sim \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6}\\ \end{pmatrix}

Kasnije će nam trebati očekivanje i varijanca te slučajne varijable (označit ću ih sa \mu i \sigma^2):
\mathbb{E} \left(X_i\right) = \mu = \frac{7}{2}
\operatorname{Var} \left(X_i\right) = \sigma^2 = \frac{35}{12}

Ono što će nama biti u fokusu jest prosjek n bacanja, gdje je n zasad nepoznat, dakle zanima nas slučajna varijabla koju ću označiti sa
Y = \frac{1}{n} \sum_{i = 1}^{n} X_i = \frac{X_1 + \dots + X_n}{n}

Distrubuciju od Y možemo odrediti centralnim graničnim teoremom, jer imamo sumu puno nezavisnih, identično distribuiranih slučajnih varijabli X_i. Prema tome, znamo da će slučajna varijabla Y aproksimativno imati normalnu razdiobu. Kako odrediti parametre (očekivanje i varijancu) od te normalne razdiobe? Vrlo jednostavno, izračunaš očekivanje i varijancu od Y:
\mathbb{E} \left(Y\right) = \mathbb{E} \left(\frac{X_1 + \dots + X_n}{n}\right) = \frac{1}{n} \ \mathbb{E} \left(X_1 + \dots + X_n\right) = \frac{1}{n} \left(\mathbb{E}\left(X_1\right) + \dots + \mathbb{E}\left(X_n\right)\right) = \frac{1}{n} \cdot n\mu = \mu \newline \operatorname{Var}\left(Y\right) = \operatorname{Var}\left(\frac{X_1 + \dots + X_n}{n}\right) = \frac{1}{n^2}\operatorname{Var}\left(X_1 + \dots + X_n\right) = \frac{1}{n^2} \left(\operatorname{Var}\left(X_1\right) + \dots + \operatorname{Var}\left(X_n\right)\right) = \frac{1}{n^2} \cdot n\sigma^2 = \frac{\sigma^2}{n}

Prilikom računanja varijance zbroja koristili smo činjenicu da su sve slučajne varijable koje se pojavljuju u zbroju (X_i -jevi od 1 do n) nezavisne, jer tek tada (točnije kad je kovarijanca 0, što je zadovoljeno kod nezavisnosti) možemo varijancu zbroja rastaviti na zbroj varijanci.
Prema tome, Y \approx \mathcal{N} \left(\mu, \frac{\sigma^2}{n}\right)

Pitanje glasi: koliko najmanje puta moramo baciti kocku da bi vjerojatnost da je aritmetička sredina dobivenih brojeva između 3 i 4 bila najmanje 0.95?
U prijevodu: koja je donja granica za n takva da vrijedi
P \left(3 < Y < 4\right) \geq 0.95.
Kako to riješiti? Zamisli kao da ovih 0.95 nemaš s desne strane, i da ti je zadatak računati ovu vjerojatnost s lijeve strane. Kako je Y normalno distribuirana, ovakav problem se rješava tako da se Y centrira i normira, odnosno da se oduzme očekivanje i podijeli sa standardnom devijacijom od Y.
P \left(\frac{3 - \mu}{\frac{\sigma}{\sqrt{n}}} < \frac{Y - \mu}{\frac{\sigma}{\sqrt{n}}} < \frac{4 - \mu}{\frac{\sigma}{\sqrt{n}}}\right) \geq 0.95
Ovo u sredini je sada jedinična normalna slučajna varijabla, odnosno \frac{Y - \mu}{\frac{\sigma}{\sqrt{n}}} \sim \mathcal{N} \left(0, 1\right), i sada možemo ovu vjerojatnost računati koristeći funkciju \Phi^*. Također primijeti kako se radi o simetričnom intervalu oko očekivanja (znamo da je očekivanje 3.5 a interval je, prije centriranja i normiranja, bio od 3 do 4), tako da gornja vjerojatnost se svodi na vrlo jednostavnih
\Phi^* \left(\frac{4 - \mu}{\frac{\sigma}{\sqrt{n}}}\right) \geq 0.95
Dakle ovdje nam je sve poznato osim n. Sad u tablici za funkciju \Phi^* pogledaš za koji argument je vjerojatnost 0.95.
Radi se o argumentu 1.96, a kako je funkcija \Phi^* rastuća, ovaj znak nejednakosti \geq ostaje takav kakav je:
\frac{4 - \mu}{\frac{\sigma}{\sqrt{n}}} \geq 1.96
Odavdje izraziš n i uvrstiš brojeve:
n \geq \left(\frac{1.96 \cdot \sigma}{4 - \mu}\right)^2 = \left(\frac{1.96 \cdot \sqrt{\frac{35}{12}}}{4 - \frac{7}{2}}\right)^2 = 44.82
Odnosno kako n mora biti prirodan: n \geq 45. Ako te zbunjuje prisutnost ovog \geq, možeš ga zamijeniti sa jednakošću i na kraju po logici odrediti jel n mora biti veći ili manji.

Jel smijemo imati podsjetnik na kpz ili ne?

Kamen
Da

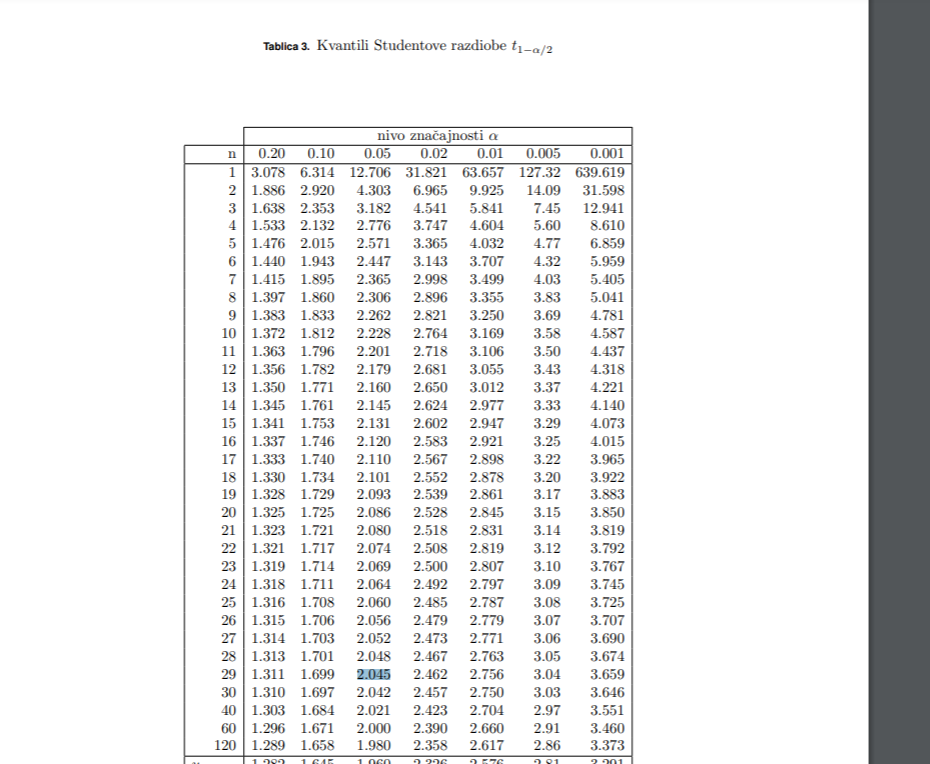
moze neko objasnit kak se cita iz ove tablice?

tetak Ti izracunas u zadatku da trazis npr t(0.95) i onda izjednacis tih 0.95 = 1 - alfa/2. Iz toga uvjeta dobijes koliki je alfa i onda u tablici trazis t od tog izracunatog alfa

Artemis
a kad je devijacija poznata pa trazim u onda samo najdoljnji red gledam pod tim alfa?