Studoši

Može li mi netko objasnit kako se računa p_j za ovo?

EDIT, shvatio, nisam ispravno našao \overline{x}.

Ne mogu naći na novim materijalima pa evo link na riješene mi/zi sa starog foruma https://mega.nz/file/OlUyFIAJ#bF3Wu4I_6jRXWFqQK0nw2sq-2AtS-uquzmtOeCyaM8c

Pineo Jel to znači da ću moć upisat SiS nagodinu drugi upis iako sam fer2 ?

caneb pa već si ga ove godine upisao kao fer3 sis tako da isto vrijedi i za sljedeću godinu

Pineo kad cemo sigurno znati je li online

Pineo kad cemo sigurno znati je li online

Ko kuži ovaj primjer? Ja ga nisam kužio prvi put kad sam učio a bome ni sad

sheriffHorsey za koja podrucja gradiva nam je korisno ovo predavanje

Mrnjotaur ovo predavanje vjerojatno za nista, al pretpostavljam da znas upalit yt, upisat “john tsitsiklis probability” i nac kaj ti treba

Ako sam izasao na završni ispiti i zimski rok
Je li sad imam pravo izaci samo na 2 od preostalih 3 (jesenski, dodatni rok i dekanski rok) ili na sva 3?

anon00 ako nisi bio na ljetnom (a po ovome nisi), onda mozes izaci na sva 3

Jel moze tko pojasniti primjer 5.4 kako dolaze do ove funkcije razdiobe i gustoće razdiobe?

Zna li netko zašto u rješenju ide ovo zaokruženo? Što ne bi trebala ići površina ovog manjeg trokuta, a ovo napisano je osnovica manjeg? Ili sam ja krivo shvatio?

Meni ispada ovako:

\LARGE\frac{\frac{av}{2}-\frac {a(v-x)^{2}}{2v}}{\frac {av}{2}}

Koje lekcije/dijelovi lekcija ne ulaze u ispit? ako uopće nešto ne ulazi

dinoo
statistika

jel R i E pisu isti ispit? jel ovo jos uvijek ne ulazi?

dinoo

[obrisani korisnik] na ljetnom smo pisali isti, ne ulazi to

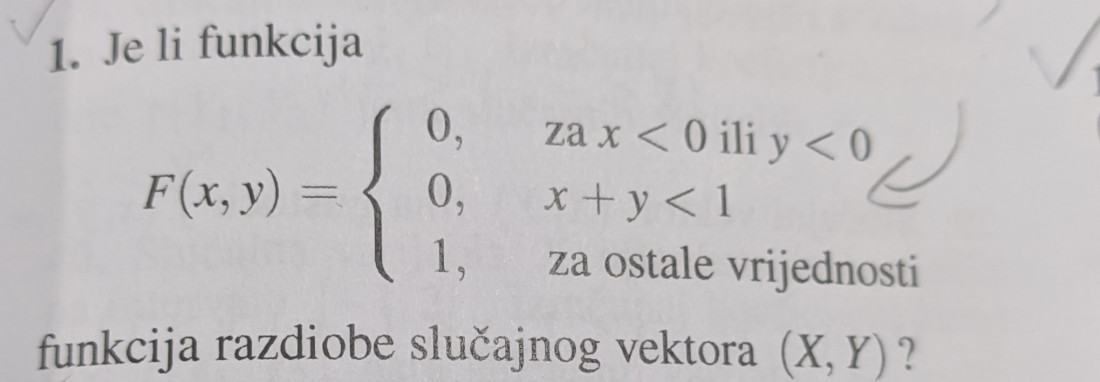
Može netko objasniti zašto je odgovor ne?

dinoo ono sto mi pada na pamet je da kad gledas po definiciji F(x,y) = P(X < x, Y < y), u svim tockama je ili 0 ili 1, ove tocke za koje je P(X < x, Y < y) = 1 znaci da je vjerojatnost 1 da je slucajna varijabla poprimila vrijednosti strogo manje od tih zadanih u (x,y), tako za svaku tocku (x,y) za koju je P=1 se spustas jer je poprimljena vrijednost strogo manja, sve dok odjednom naglo ne dode do tocke za koju je P=0, dakle nju ne moze isto poprimit a ne moze ni jednu manju od nje, po definiciji

drugim rijecima, u funkciji razdiobe, izmedu poprimanja vrijednosti 0 i 1 uvijek mora postojat jos neka vrijednost koju vjerojatnost poprima, to jer je F(x) = P(X < x) a ne = P(X <= x)
(ako se ne varam)

Zasto ovaj P \left(Y >\frac{1-z}zX \right) prelazi u integral sa f_{x} \left(x \right), i zasto se za z izmedu 1 i +\infty
samo gleda f_{x} \left(x \right) ?

Kuhar Zero

Iskreno da vam kažem, trebalo mi je otprilike 2 sata gledanja u ovo rješenje da bih shvatio na koji način su oni to riješili, pa ću vam cijeli postupak isprezentirati od početka do kraja.

Ok, znači znamo da su X i Y nezavisne slučajne varijable sa istom, eksponencijalnom razdiobom sa parametrom \lambda = 1. Iz toga odmah možemo saznati njihove funckije gustoće f_X\left(x\right), f_Y\left(y\right) i funkcije distribucije (koje će nam trebati kasnije) F_X\left(x\right), F_Y\left(y\right).

Općenito, nevezano za zadatak, ako je X neka eksponencijalna slučajna varijabla sa parametrom \lambda > 0, odnosno
X \sim \mathscr{E}\left(\lambda\right)
tada su njene funkcije gustoće f_X\left(x\right) i distribucije F_X\left(x\right):
f_X\left(x\right) = \begin{cases} \lambda e^{-\lambda x} & \text{za} \ x > 0 \\ 0 & \text{inače} \\ \end{cases}

F_X\left(x\right) = \begin{cases} 1 - e^{-\lambda x} & \text{za} \ x > 0 \\ 0 & \text{inače} \end{cases}

ovo zadnje se izvede iz prvog jednostavnim integralom F_X\left(x\right) = \int_{-\infty}^{x} f_X\left(u\right) \mathrm{d}u po definiciji u slučaju da zaboravite.

U našem slučaju:
f_X\left(x\right) = \begin{cases} e^{-x} & \text{za} \ x > 0 \\ 0 & \text{inače} \\ \end{cases} \qquad f_Y\left(y\right) = \begin{cases} e^{-y} & \text{za} \ y > 0 \\ 0 & \text{inače} \\ \end{cases}

F_X\left(x\right) = \begin{cases} 1 - e^{-x} & \text{za} \ x > 0 \\ 0 & \text{inače} \end{cases} \qquad F_Y\left(y\right) = \begin{cases} 1 - e^{-y} & \text{za} \ y > 0 \\ 0 & \text{inače} \end{cases}

Okej, sad se pitamo sljedeće:
Dobro, ja sad znam kakve razdiobe imaju X i Y, ali na koju jebenu foru da znam (dobro aj znam da je uniformna, ali kako da dokažem) kakvu razdiobu ima slučajna varijabla Z = \frac{X}{X+Y} ?
Well odgovor ćemo naći ako pokušamo naći njenu funkciju distribucije F_Z\left(z\right) koju računamo po definiciji:
F_Z\left(z\right) = P \left(Z < z\right)
Interpretacija: koja je vjerojatnost da moja slučajna varijabla Z (veliko slovo, što znači slučajna varijabla) poprimi vrijednost manju od nekog odabranog broja z (malo slovo, što znači argument funkcije, odnosno nešto što pretpostavljamo da nam je poznato unaprijed, unlike slučajna varijabla koja nije poznata unaprijed) ?
Vještim manevriranjem dolazimo do sljedećeg:
F_Z\left(z\right) = P \left(Z < z\right) = P \left(\frac{X}{X + Y} < z\right) \newline \qquad = P \left(X < z\left(X + Y\right)\right) = P \left(X < zX + zY\right) = P \left(zY > X - zX\right) \newline \qquad = P \left(Y > \frac{1 - z}{z} X\right)

E sad ovdje morate paziti da ne šamarate te nejednakosti kako se vama sprdne. Ovdje smo koristili činjenicu da slučajne varijable X i Y mogu poprimiti isključivo strogo pozitivne vrijednosti (kad smo množili nejednakost sa X + Y da znak nejednakosti ostane isti), a u zadnjem koraku smo odlučili razmatrati slučaj samo ako je argument z strogo pozitivan, da opet znak nejednakosti ostane kakav je bio. Slučaj koji nismo time pokrili, z \leq 0 ćemo razmotriti kasnije.

I sad su se oni odlučili za jedan epski gamer move i koristili su formulu iz Elezovićevog udžbenika ViS Slučajne varijable: dno stranice 70, formula 7.3 koja kaže:

Ako ja imam neki događaj A čija vjerojatnost P \left(A\right) mi ovisi o tome kakvu vrijednost će poprimiti slučajna varijabla X, tada takvu vjerojatnost mogu računati tako da prvo nađem uvjetnu vjerojatnost P \left(A \mid X = x\right): vjerojatnost tog istog događaja A ako ja unaprijed znam koliku vrijednost će mi slučajna varijabla X poprimiti (to je ovaj dio “\mid X = x”), što je obično lakši posao. E onda kad sam našao tu uvjetnu vjerojatnost, i znam funkciju gustoće slučajne varijable X, e onda mogu zveknut ovakav integral:
P \left(A\right) = \int_{-\infty}^{+\infty} P \left(A \mid X = x\right) f_X\left(x\right) \mathrm{d}x
s tim da se ove granice integracije ravnaju prema tome kako i gdje je definirana funkcija gustoće f_X\left(x\right).

U našem slučaju, naš događaj A iz formule koji ovisi o tome kakvu vrijednost će poprimiti X je upravo događaj Y > \frac{1 - z}{z} X. Nas zanima P \left(Y > \frac{1 - z}{z} X\right), e al kada bismo znali koliko točno iznosi slučajna varijabla X i rekli neka je on jednak malom x(onaj dioX = x), e onda bi se takva vjerojatnost (sada uvjetna, P \left(Y > \frac{1 - z}{z} X \mid X = x\right), odnosno P \left(Y > \frac{1 - z}{z} x\right)) lako računala jer je s desne strane nejednakosti sada neki realan broj, a to možemo lako računati koristeći funkciju distribucije F_Y \left(y\right).

Nastavimo dalje gdje smo stali:

F_Z\left(z\right) = P \left(Y > \frac{1 - z}{z} X\right) \newline \qquad = \int_{-\infty}^{+\infty} P \left(Y > \frac{1 - z}{z} x\right) f_X\left(x\right) \mathrm{d}x
Zbog toga što funkcija gustoće f_X\left(x\right) nije nula samo za pozitivne x, granice integracije promijenimo u od 0 do +\infty. Uz to, vrijedi i sljedeće: P \left(Y > \frac{1 - z}{z} x\right) = 1 - P \left(Y < \frac{1 - z}{z} x\right) = 1 - F_Y \left(\frac{1 - z}{z} x\right). Tu smo koristili činjenicu da je Y kontinuirana slučajna varijabla (vjerojatnost događaja jednakosti je 0) i iskoristili smo definiciju funkcije razdiobe.

F_Z\left(z\right) = P \left(Y > \frac{1 - z}{z} X\right) \newline \qquad = \int_{-\infty}^{+\infty} P \left(Y > \frac{1 - z}{z} x\right) f_X\left(x\right) \mathrm{d}x \newline \qquad = \int_{0}^{+\infty} \left(1 - F_Y \left(\frac{1 - z}{z} x\right)\right) e^{-x} \mathrm{d}x

Sad moramo pravilno evaluirati F_Y \left(\frac{1 - z}{z} x\right). Ako se sjetimo kako izgleda funkcija razdiobe F_Y \left(y\right) naše eksponencijalne varijable Y, onda ćemo zaključiti da funkcija nije nula samo za pozitivne argumente. Dakle promatramo argument \frac{1 - z}{z} x i gledamo njegov predznak. Za početak, znamo da smo u domeni integracije pozitivnih x pa se za to ne trebamo brinuti. Ostaje nam gledati predznak izraza \frac{1 - z}{z}. Srednjoškolskim manevriranjem ovakvog trivijalnog pitanja zaključujemo da će biti strogo pozitivno ukoliko je 0 < z < 1. U tom slučaju možemo sa sigurnošću tvrditi da je F_Y \left(\frac{1 - z}{z} x\right) = 1 - e^{-\frac{1 - z}{z} x}, iz čega slijedi jedan od slučajeva:

F_Z\left(z\right) = \int_{0}^{+\infty} \left(1 - \left(1 - e^{-\frac{1 - z}{z} x}\right)\right) e^{-x} \mathrm{d}x \newline \qquad = \int_{0}^{+\infty} e^{-x \left(\frac{1 - z}{z} + 1\right)} \mathrm{d}x \newline \qquad = \int_{0}^{+\infty} e^{-\frac{x}{z}} \mathrm{d}x = -z e^{-\frac{x}{z}} \biggr|_{x=0}^{x \to +\infty} \newline \qquad = z \qquad \text{za} \ 0 < z < 1

A sad ako z nije iz tog intervala (ali opet unutar onog našeg na početku gdje smo manevrirali sa nejednakostima i rekli da ćemo slučaj z \leq 0 razmatrati kasnije jer tada ne zadržavamo isti znak nejednakosti), odnosno ako je z \geq 1 onda znamo da je cijeli izraz \frac{1 - z}{z} x negativan (ili 0), stoga će vrijediti F_Y \left(\frac{1 - z}{z} x\right) = 0.
Tada imamo još jedan slučaj:

F_Z\left(z\right) = \int_{0}^{+\infty} \left(1 - \left(1 - 0\right)\right) e^{-x} \mathrm{d}x = \int_{0}^{+\infty} e^{-x} \mathrm{d}x = 1 \qquad \text{za} \ z \geq 1

Sad napokon idemo razmotriti onaj slučaj, što ako je z \leq 0?
Da bismo dobili odgovor na to, vratimo se nazad na početak raspisivanja funkcije razdiobe F_Z \left(z\right):

F_Z\left(z\right) = P \left(Z < z\right) = P \left(\frac{X}{X + Y} < z\right)

I zapitajmo se, kolika je vjerojatnost, je li to uopće moguće, da izraz s lijeve strane nejednakosti \frac{X}{X + Y} bude manji od nečeg što je 0 ili strogo negativno (z) ? Pa naravno da ne, jer eksponencijalne slučajne varijable X i Y mogu poprimiti samo strogo pozitivne vrijednosti, stoga će i \frac{X}{X + Y} uvijek biti isključivo strogo pozitivan. Dakle ta vjerojatnost je 0.

F_Z\left(z\right) = P \left(Z < z\right) = P \left(\frac{X}{X + Y} < z\right) = 0 \qquad \text{za} \ z \leq 0

I onda naša funkcija razdiobe F_Z\left(z\right) u konačnici izgleda ovako:

F_Z \left(z\right) = \begin{cases} z & \text{za} \ 0 < z < 1 \\ 1 & \text{za} \ z \geq 1 \\ 0 & \text{za} \ z \leq 0 \end{cases}

Čak nije ni bitno gdje je jednakost a gdje nije jer u svakom slučaju je funkcija neprekidna.
I je li to stvarno liči na slučajnu varijablu uniformne razdiobe, odnosno je ii Z \sim \mathscr{U}(0, 1) ? Pa jest, u to se dodatno možemo uvjeriti ako deriviranjem funkcije razdiobe izračunamo funkciju gustoće f_Z \left(z\right) = \frac{\mathrm{d} F_Z}{\mathrm{d}z} \left(z\right)

f_Z \left(z\right) = \begin{cases} 1 & \text{za} \ 0 < z < 1 \\ 0 & \text{inače} \end{cases}

Sad ovakav način i onakvu formulu ja iskreno ne bih nikad iskoristio, jer samo komplicira stvari, a nema ništa lakše od good old šablone, koja je za ovakav tip zadataka naći gustoću vektora nezavisnih slučajnih varijabli: f_{X, Y} \left(x, y\right) = f_X \left(x\right) f_Y \left(y\right) (paziti na područja definiranosti) i onda vjerojatnost P \left(Y > \frac{1 - z}{z} X\right) računati dvostrukim integralom \int_{0}^{+\infty} \mathrm{d}x \int_{\frac{1 - z}{z} x}^{+\infty} f_{X, Y} \left(x, y\right)\mathrm{d}y. Doduše ovdje bi opet trebalo paziti na predznake i u kojem području integriramo ali opet lakše za shvatiti nego njihovo.

Zna li netko koja točno gradiva ne ulaze u ispit? U Lenkinoj obavijesti na FERWebu ima dosta naslova kojih nema u knjizi pa ne znam što mogu preskočiti