[MEKRAC] Gradivo
Ducky
Daeyarn 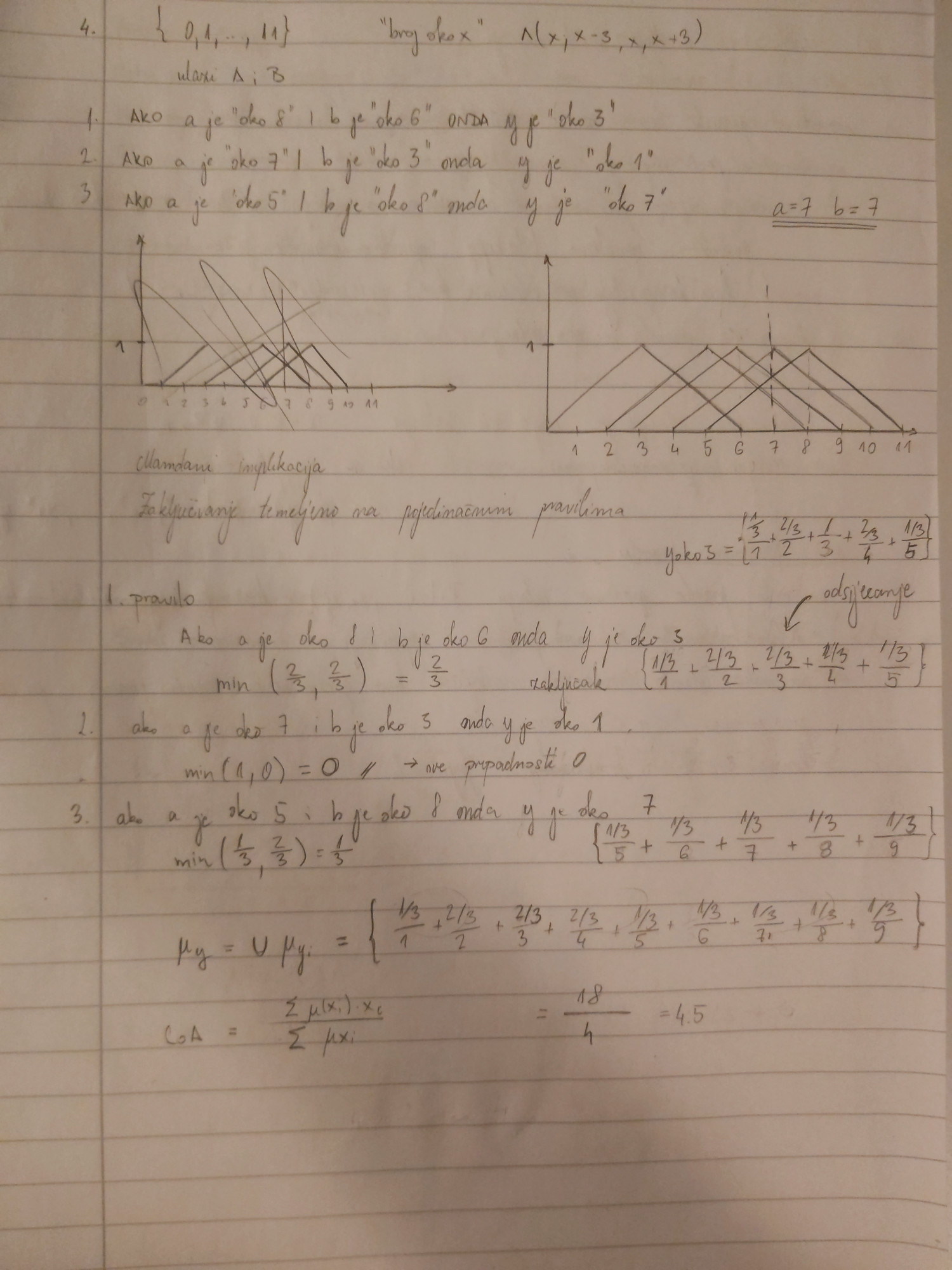
evo rješenje od prošle godine.
10 minuta sam pokušavao shvatiti otkud cilindrično proširenje. Jel možeš pliz elaborirat?
Daeyarn
Ducky maa zabrijao sam nekj, mislio sam da se treba tipa za prvo pravilo napisati neizraziti skupovi a je oko 8 i b je oko 6, i onda njih spojiti u relaciju operatorom I, i onda napraviti kartezijev produkt te relacije i skupa y je oko 3, i onda konacni neizraziti skup izracunat kao kompoziciju s ulazom
nisam razmisljao da se samo konkretno izracuna vrijednost od a je oko 8 za a=7 I b je oko 6 za b=7, i onda kartezijev produkt tog broja sa y je oko 6(usporedivanje sa svakim elementom iz y je oko 3 i uzimanje minimuma)
hvala na rjesenju!!!
Ducky
Daeyarn aha, oke. Also jel
za prvo pravilo napisati neizraziti skupovi a je oko 8 i b je oko 6, i onda njih spojiti u relaciju operatorom I, i onda napraviti kartezijev produkt te relacije i skupa y je oko 3, i onda konacni neizraziti skup izracunat kao kompoziciju s ulazom
to možda odgovor na a dio zadatka? (postupak zaključivanja temeljeno na kompoziciji)
Daeyarn
Ducky msm da da, ali sam i bio krivo skuzio sto treba u b) raditi
bodilyfluids
Koja je ideja s selekcijom kod genetskih algoritama? Recimo za generacijske algoritme. Recimo da je veličina populacije 100. Jel ideja da prvo od tih 100 selektiramo neki dio, npr. 40 i onda nasumično 100 puta biramo dvije jedinke od selektiranih i tako dobivamo novu populaciju?
A kod eliminacijskih prvo eliminiramo dio, i onda od preživjele populacije opet random 100 puta uzimamo par koji stvara novu jedinku?
Pretpostavljam da se može napravit na svakakve načine, ali jesam dobro shvatio da je ovo gore način koji su nam na predmetu prezentirali?
tonkec
Dragi prijatelj strojnog učenja Za ovaj prvi dio ako uzmeš npr. roulette wheel selekciju, “zavrtiš” dvaput (možda još koji put ako odabreš dvije iste jedinke) to kolo nad cijelom populacijom i dobiješ dva roditelja. Križaš ta dva roditelja i dobiješ jedno ili dvoje djece (ovisi o križanju) i onda možeš dodati dvije najbolje od te tri (četiri) u novu populaciju. Taj proces radiš do kada ne popuniš sve pozicije u novoj populaciji, a tih pozicija je koliko ti je veličina pupulacije.
Za ovaj drugi dio bi mogao napraviti sort populacije po dobroti jedinki, ubiti goru polovicu pa onda preostale koristiti za stvaranje nove populacije. Drugi način kako možeš je umjesto da koristiš samo bolju polovicu za stvaranje nove generacije, izgeneriraš onoliko novih jedinki koliko si ubio i onda sve zajedno koristiš za stvaranje nove populacije.
Rene
tonkec oprezno s ovim drugim, tu imas dosta velik selekcijski pritisak gdje u startu odbacis dosta rjesenja (pogotovo problematicno na pocetku kad su sva rjesenja relativno losa) tako da nije najbolja taktika. Npr. k-turnirska selekcija nasumicno bira iz svih, s tim da ce losije vjerojatnije biti eliminirane
bodilyfluids
upomoc

angello2
Dragi prijatelj strojnog učenja ma nebu to valjda pito hahahah
Rene
Dragi prijatelj strojnog učenja
Neku shemu možeš “uništit” na dva načina: križanjem i mutacijom; selekcija ne utječe na to jer ne mijenja jedinku.
Vjerojatnost da ćeš uništit shemu križanjem proporcionalna je definiranoj dužini (jer što je veći razmak između fiksnih znakova, to između njih ima više mjesta na kojem možeš napravit promjenu) i vjerojatnosti križanja, a obrnuto proporcionalna broju mogućih točaka prekida. Primjer: sheme su *11** i 1***1. Neka je križanje s jednom točkom prekida i neka križaš s 00000. Prvu shemu ćeš sjebat ako je točka prekida na 2. mjestu, a drugu ako je na 1. ili 2. ili 3. ili 4. mjestu.
Vjerojatnost da ćeš uništit shemu mutacijom je proporcionalna redu sheme(jer mutacija će uništit shemu ako mutiraš fiksni gen, a broj fiksnih gena je o(S)) i vjerojatnosti mutacije. To je drugi član koji se oduzima na desnoj strani.
Znači očekivani broj rješenja koje su podskup sheme S će rasti s ovim faktorom \frac{\bar{D_s}}{\bar{D}} jer su iznadprosječno dobre, pa će više preživljavat, ali umanjeno za ove slučajeve kada će se shema uništit križanjem i mutacijom. Ngl nije ni meni najbistrije u glavi, ali valjda će ti pomoć
bodilyfluids
Kako učite za MI nakon što ste prošli MI 2017?
Jaster111
Kako riješiti 4.b) ako bi nam bilo zadano zaključivanje temeljeno na kompoziciji, a ne na pravilima?
bodilyfluids
Jaster111 ispravite me ako sam u krivu, ovako sam shvatio razliku:
Temeljeno na kompoziciji:
stvori pravila -> napravi spoj pravila -> kompozicija(ulaz, spojena pravila) -> defuzzify rezultat kompozicije
Temeljeno na pojedinačnim pravilima:
stvori pravila -> za sva pravila napravi kompozicija(ulaz, pojedinačno pravilo) -> spoji rezultate, tj. kompozicije -> defuzzify spojene kompozicije
Dakle u prvom slučaju spajaš pravila i dobiš jedan zaključak, u drugom slučaju ne spajaš pravila, pa imaš više zaključaka koje prvo treba spojit pa defazificirat.
Nevezano za pitanje ali primjeti kako sam oprezno koristio riječ “spoj” relacija. Spajanje radiš presjekom ili unijom, ovisno o tome koristiš li lokalna ili globalna pravila zaključivanja.
AK10
iz cega uciti evolucijsko? vidim da tipa ovo kruzno krizanje nema u prezentacijama
bodilyfluids
endyyyy evolucijsko uči s prezentacije, vjerojatno je došlo do promjena u gradivu od 2017 do sada.
AK10
Dragi prijatelj strojnog učenja
dakle vidim da je bio cycle crossover u mi 2017 a nama je to sivi slajd? sta kao to nama onda nece bit, jel na to mislis da je doslo do promjena u gradivu od 2017 do sada?
bodilyfluids
endyyyy da, valjda se gradivo malo promijenilo.
ovdje sam napisao još malo o sivim slajdovima, Dragi prijatelj strojnog učenja
Emma63194
Dragi prijatelj strojnog učenja Ne znam koliko je efikasno, ali u teoriji možeš napraviti kompoziciju relacije same sa sobom i ako se nešto promijeni u rezultantnoj relaciji, onda znaš da ti ova početna nije bila tranzitivna (ne mora ni dobivena nužno biti, ali to sada nije bitno).
feel_d_boot
Dragi prijatelj strojnog učenja
Emma63194
Zar ovo nije samo u slučaju kad je početna relacija refleksivna i simetrična?
Napraviš jednu kompoziciju relacije same sa sobom pa ako je rezultantna relacija ista kao početna, onda ima svojstvo tranzitivnosti. Ako nije, znaš da početna relacije nema svojstvo tranzitivnosti.
Ne znam koliko sam dobro objasnija, al na 65. stranici skripte (77 od 291) ima jednostavno objašnjeno i kad relacija ima svojstva simteričnosti i refleksivnosti i kad ih nema.

EDIT: OBAVEZNO me ispravite ako sam nešto krivo napisa da ne bih sjeba nekoga ubuduće.
Emma63194
iNut Zar ovo nije samo u slučaju kad je početna relacija refleksivna i simetrična?
Vidiš, nisam sada 100% sigurna oko toga.
iNut Napraviš jednu kompoziciju relacije same sa sobom pa ako je rezultantna relacija ista kao početna, onda ima svojstvo tranzitivnosti. Ako nije, znaš da početna relacije nema svojstvo tranzitivnosti.
Isto smo napisali, da, samo ja nisam uzela u obzir mora li relacija biti relacija kompatibilnosti ili ne.
iNut Ne znam koliko sam dobro objasnija, al na 65. stranici skripte (77 od 291) ima jednostavno objašnjeno i kad relacija ima svojstva simteričnosti i refleksivnosti i kad ih nema.
Kaže da se tranzitivno zatvaranje može ostvariti kao unija relacije dignute na potencije od 1 do beskonačno.
Ako se dobro sjećam, potenciranje opet uključuje kompoziciju.
Ne znam može li se desiti da je relacija nesimetrična i nerefleksivna, ali tranzitivna pa da se onda kompozicijom same sa sobom dobije nova relacija (dakle, različita od početne). Iz toga bismo po onom mojem prvom dobili da je netranzitivna, iako je zapravo bila i da, onda ne bi vrijedila takva provjera tranzitivnosti.
Mislim da kompozicija relacije same sa sobom ne bi trebala pogoršati svojstvo tranzitivnosti, ali nisam sigurna bi li popravila svojstvo refleksije i simetričnosti. Moj guess je da ne bi, ali najbolje profesora pitati još oko ovoga.