Studoši

iNut Zar ovo nije samo u slučaju kad je početna relacija refleksivna i simetrična?

Vidiš, nisam sada 100% sigurna oko toga.

iNut Napraviš jednu kompoziciju relacije same sa sobom pa ako je rezultantna relacija ista kao početna, onda ima svojstvo tranzitivnosti. Ako nije, znaš da početna relacije nema svojstvo tranzitivnosti.

Isto smo napisali, da, samo ja nisam uzela u obzir mora li relacija biti relacija kompatibilnosti ili ne.

iNut Ne znam koliko sam dobro objasnija, al na 65. stranici skripte (77 od 291) ima jednostavno objašnjeno i kad relacija ima svojstva simteričnosti i refleksivnosti i kad ih nema.

Kaže da se tranzitivno zatvaranje može ostvariti kao unija relacije dignute na potencije od 1 do beskonačno.
Ako se dobro sjećam, potenciranje opet uključuje kompoziciju.

Ne znam može li se desiti da je relacija nesimetrična i nerefleksivna, ali tranzitivna pa da se onda kompozicijom same sa sobom dobije nova relacija (dakle, različita od početne). Iz toga bismo po onom mojem prvom dobili da je netranzitivna, iako je zapravo bila i da, onda ne bi vrijedila takva provjera tranzitivnosti.

Mislim da kompozicija relacije same sa sobom ne bi trebala pogoršati svojstvo tranzitivnosti, ali nisam sigurna bi li popravila svojstvo refleksije i simetričnosti. Moj guess je da ne bi, ali najbolje profesora pitati još oko ovoga.

Emma63194 Kaže da se tranzitivno zatvaranje može ostvariti kao unija relacije dignute na potencije od 1 do beskonačno.
Ako se dobro sjećam, potenciranje opet uključuje kompoziciju.

Ovo beskonačno je čisto tu teorije radi, nama kurca ne vridi. Zaboravija sam napomeniti da se to koristi samo ako je univerzalni skup konačan. A potencija relacije je zapravo koliko put radiš kompoziciju te relacije same sa sobom.

Emma63194 Ne znam može li se desiti da je relacija nesimetrična i nerefleksivna, ali tranzitivna pa da se onda kompozicijom same sa sobom dobije nova relacija (dakle, različita od početne). Iz toga bismo po onom mojem prvom dobili da je netranzitivna, iako je zapravo bila i da, onda ne bi vrijedila takva provjera tranzitivnosti.

Mislim da kompozicija relacije same sa sobom ne bi trebala pogoršati svojstvo tranzitivnosti, ali nisam sigurna bi li popravila svojstvo refleksije i simetričnosti. Moj guess je da ne bi, ali najbolje profesora pitati još oko ovoga.

Čisto se želim i ja nadovezati na to da nisam ni ja siguran oko toga, pa bi bilo najbolje za to (ako ovo čitaš u budućnosti) pitati profesora na predavanjima ili otići na konzultacije jer na mail neće odgovoriti.

Kako se u eliminacijskom algoritmu shvaća mortalitet?

Npr ako je M=50% ka što je preporučeno po literaturi, shvaćam li to onda kao da trebam eliminirati 50 posto populacije prije nego što započne reprodukcija?

iNut Tako je - prvo odabireš jedinke koje ćeš ubiti, s tim da ti lošije jedinke u eliminacijskom algoritmu za to imaju više šanse, a onda te ubijene nadomjestiš križanjem preostalih.

iNut

Ovo kaj kaže M̵̧̩͑̀͝î̶͍̉ć̴̝̾́̀o̶̺̟̣͂̽ , ali treba imat na umu da kod evolucijskih algoritama ima hrpa varijanti za svaki operator, npr. u tekstu 4. zadatka:

kanonski eliminacijski genetski algoritam (jednostavna troturnirska selekcija: biramo tri
jedinke, dvije bolje su roditelji, nastalo dijete zamjenjuje preostalog/trećeg najlošijeg
roditelja).

Ovo se može tumačiti da čim jedna jedinka krepa, dvije preživjele odma stvaraju dijete koje se ubacuje u populaciju. I sad je pitanje što koristiti? Pa to ovisi o ostalim operatorima i domeni problema kojeg rješavaš, odnosno o selekcijskom pritisku.

Ko god se sjeca cupicevih zadataka na predavanjima ili hintova što bi moglo doći na ispitu, slobodno podijelite :')

Evo za pocetak:
Zadnji sat se radio fuzzy k-means, i biti ce vrlo vjerojatno zadatak da izvrtimo jednu iteraciju za dani skup primjera.

Dragi prijatelj strojnog učenja Ne mogu se sjetiti i ne znam je li vrijedi, ali mislim da je spominjao kako se moze na usmenom pojaviti zadatak kao iz 8.1 gdje moramo odrediti/izvesti za koje vrijednosti ce konvergirati, alternativno divergirati i divergirati

Dragi prijatelj strojnog učenja

Evo ovdje jedan pdf, sadrži zadatke za vježbu iz nekih dijelova gradiva drugog ciklusa: https://docdro.id/Td1yOwu

Ovo je jedan zadatak iz zadnjeg dijela gradiva:

Dragi prijatelj strojnog učenja
Čini mi se da je profesor spominjao da bi ovako nešto moglo doću u ZI:

Znači, zadano tako neko stablo i izvesti pravila onda.
Inače, to je 13. lekcija (Oblikovanje i učenje neuronske mreže algoritmima evolucijskog računanja) iz knjige.

branimir1999 usmenom?? govoriš o roku ili?

[obrisani korisnik] Da, samo na roku, Zato sam i rekao “ne znam je li vrijedi” i navodim ga jer je profesor eksplicitno spomenuo taj zadatak

Ima li negdi primjer zi-a od prošlih godina?

iNut ima na materijalima ali ne znam koliko je relevantan za ovu godinu, pola tog ispita je prvi ciklus

U ovom dokumentu za vježbu, u zadatku 6., izraz za izlaz neurona je dan na sljedeći način: .
Vidimo da se ova “fiktivna” težina (w7), tj. prag neurona oduzima od ukupne sume net. Međutim, koliko vidim u knjizi, taj prag se samo zbraja sa ostalim težinama:

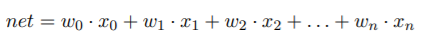
Pa me zanimalo zna li itko je li to greška u rješenjima zadatka ili sam ja samo predvidio nešto očito 😅

indythedog mislim da je samo stvar zapisa, mozes uzeti -w0 ili +w0×0 i rec da je x0=-1

DnkCkv Aha, znači u svakom slučaju ili w0 ili x0 moraju biti -1? To odgovara ovom što piše u dokumentu ali u knjizi su npr. stavili da su i w0 i x0 oba pozitivni hm

Emma63194
Ima li negdi ovakav riješen primjer s objašnjenjem?

Jel bi mogao netko malo pojasnit sta se dogada ovdje u svakom od slojeva? Zahvaljujem!

BaboTrojka prvi sloj modelira jezicne izraze, tj. one neizrazite skupove za x i y
neuroni oznaceni s TT racunaju t-normu, dakle kombiniraju antecedent pravila: prvi neuron - Ako je X A1 I Y je B1, drugi neuron - Ako je X A2 I Y JE B2. Treci sloj normira tezine, racuna \frac{w_1}{w_1+w_2} odnosno \frac{w_2}{w_1+w_2} . Te tezine w su zapravo rezultat t normi proslog sloja, a ovo racunas jer kod TSK zakljucivanja izlaz je \hat{w_1}f_1 + \hat{w_2}f_2 . Predzadnji sloj racuna te funkcije f i mnozi ih s normiranim tezinama, i zadnji konacno to sve zbraja.

Emma63194 Lekcije 7, 8, 9, 12, 13 i 14.

Gdje je lekcija 8? Ne vidim to predavanje na ferku.
Ili je to samo u knjizi?

yabk
Nema na ferku, samo u knjizi, a na predavanja nisam iša pa ti ne znam više reći.

yabk profesor je backprop izvodio uživo na predavanju, nije koristio nikakve materijale, al nisi ništa propustio jer je sve napisano u knjizi